Trong tam giác vuông có hai cạnh góc vuông là a, b; góc đối diện với cạnh a là α ; góc đối diện với cạnh b và β và cạnh huyền là c. Hãy tìm khẳng định đúng
A. a = csin α B. a = ccos α
C. a = ctg α D. a = ccotg α
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi độ dài cạnh góc vuông nhỏ hơn của tam giác vuông đó là x (cm); (0 < x < 20)
Cạnh góc vuông lớn hơn của tam giác vuông có độ dài là: x + 4
Vì cạnh huyền bằng 20 cm nên theo định lý Py-ta-go ta có:
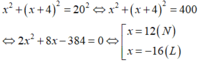
Vậy độ dài hai cạnh góc vuông của tam giác vuông đó lần lượt là: 12 cm và 12 + 4 = 16 cm

Đáp án A
Gọi độ dài cạnh góc vuông nhỏ hơn của tam giác vuông đó là x (cm); (0 < x < 20)
Cạnh góc vuông lớn hơn của tam giác vuông có độ dài là: x + 4
Vì cạnh huyền bằng 20 cm nên theo định lý Py-ta-go ta có:
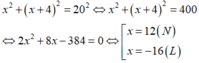
Vậy độ dài hai cạnh góc vuông của tam giác vuông đó lần lượt là: 12 cm và 12 + 4 = 16 cm

Bài 1:
\(S=\dfrac{2.4\cdot1.7}{2}=1.2\cdot1.7=2.04\left(dm^2\right)\)
Bài 2:
\(S=\dfrac{24\cdot16}{2}=24\cdot8=192\left(cm^2\right)\)
Chọn đáp án A