Cho hình thang vuông ABCD (AB//CD;góc A = góc D =90 độ)Tia phân giác góc C đi qua trung điểm M của AD.Gọi E là hình chiếu của M trên BC.Tính góc AED
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kẻ \(AH;BK\) vuông góc với DC (H,K thuộc DC)
Xét \(\Delta\) AHD và \(\Delta\)BKC:
\(\widehat{AHD}=\widehat{BKC}=90^0\)
AD=BC( do ABCD là hình thang cân)
\(\widehat{D}=\widehat{C}\) (Hai góc cùng kề một đáy trong htc)
nên \(\Delta\)AHD=\(\Delta\)BKC(ch-gn) \(\Rightarrow DH=KC\)
Có AB//DC và AH//BK => ABKH là hbh => AB=HK
Có \(DH+HK+KC=DC\) \(\Leftrightarrow2KC+AB=DC\Leftrightarrow KC=\dfrac{50-14}{2}=18\) (cm)
Áp dụng hệ thức trong tam giác vuông CDB có:
\(BK^2=DK.KC\Leftrightarrow BK=\sqrt{DK.KC}=\sqrt{\left(DC-KC\right).KC}=24\) (cm)
Diện tích hình thang là: \(S=\dfrac{1}{2}BK\left(AB+CD\right)=\dfrac{1}{2}.24\left(14+50\right)=768\) (cm2)

. a) HS tự chứng minh
b) Kẻ đường cao AH, BK,chứng minh được DH = CK
Ta được H D = C D − A B 2 = 3 c m
Þ AH = 4cm Þ SABCD = 20cm2

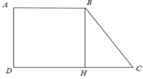
Xét hình thang ABCD
Từ B kẻ BH ⊥ CD, khi đó ta được hình chữ nhật ABHD ⇒ AB = DH = 2cm
⇒ HC = CD - DH = 4 - 2 = 2cm.
+ Xét Δ BDC có BH là đường cao đồng thời là đường trung tuyến
⇒ Δ BDC là tam giác cân tại B.

Chọn đáp án D.

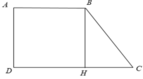
Xét hình thang ABCD
Từ B kẻ BH ⊥ CD, khi đó ta được hình chữ nhật ABHD ⇒ AB = DH = 2cm
⇒ HC = CD - DH = 4 - 2 = 2cm.
+ Xét Δ BDC có BH là đường cao đồng thời là đường trung tuyến
⇒ Δ BDC là tam giác cân tại B.

Chọn đáp án D.

Kẻ đường cao BE \(\Rightarrow BE=12\)
Pitago tam giác vuông BDE:
\(DE=\sqrt{BD^2-BE^2}=9\left(cm\right)\)
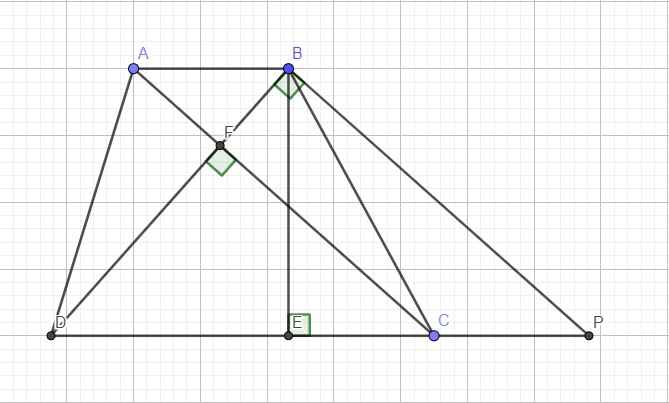
Qua B kẻ đường thẳng song song AC cắt CD kéo dài tại P
Do \(AC\perp BD\Rightarrow BP\perp BD\) hay tam giác BPD vuông tại B
Mặt khác \(\left\{{}\begin{matrix}AB||CD\\AC||BP\end{matrix}\right.\) \(\Rightarrow ABPC\) là hbh
\(\Rightarrow AB=CP\Rightarrow AB+CD=CP+CD=DP\)
Hệ thức lượng tam giác vuông BPD:
\(BD^2=DE.DP\Rightarrow DP=\dfrac{BD^2}{DE}=25\left(cm\right)\)
\(S_{ABCD}=\dfrac{1}{2}BE.\left(AB+CD\right)=\dfrac{1}{2}BE.DP=\dfrac{1}{2}.9.25=112,5\left(cm^2\right)\)