Cho các số thực a;b;c;d;e khác 0 thỏa mãn : \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{d}{e}\) . Chứng minh rằng : \(\dfrac{2a^4+3b^4+4c^4+5d^4}{2b^4+3c^4+4d^4+5e^4}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
7 tháng 5 2018
Chọn C.
Phương pháp: Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải:


CM
25 tháng 3 2019
Giả sử phương trình đã cho có 3 nghiệm
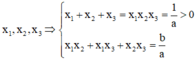
Khi đó
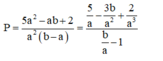
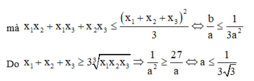
Suy ra
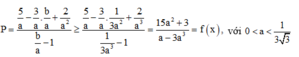
Xét hàm số:
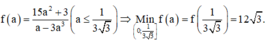
Chọn D.

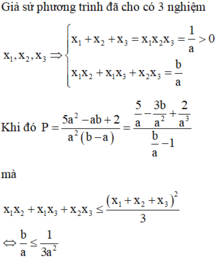
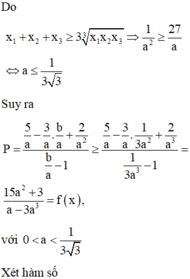
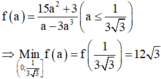
ta có: \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{d}{e}\Rightarrow\dfrac{a^4}{b^4}=\dfrac{b^4}{c^4}=\dfrac{c^4}{d^4}=\dfrac{d^4}{e^4}\)
\(\dfrac{2a^4+3b^4+4c^4+5d^4}{2b^4+3c^4+4d^4+5e^4}=\dfrac{2a^4}{2b^4}=\dfrac{3b^4}{3c^4}=\dfrac{4c^4}{4d^4}=\dfrac{4d^4}{4e^4}\\ =\dfrac{a^4}{b^4}=\dfrac{b^4}{c^4}=\dfrac{c^4}{d^4}=\dfrac{d^4}{e^4}\\ \dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{d}{e}\)