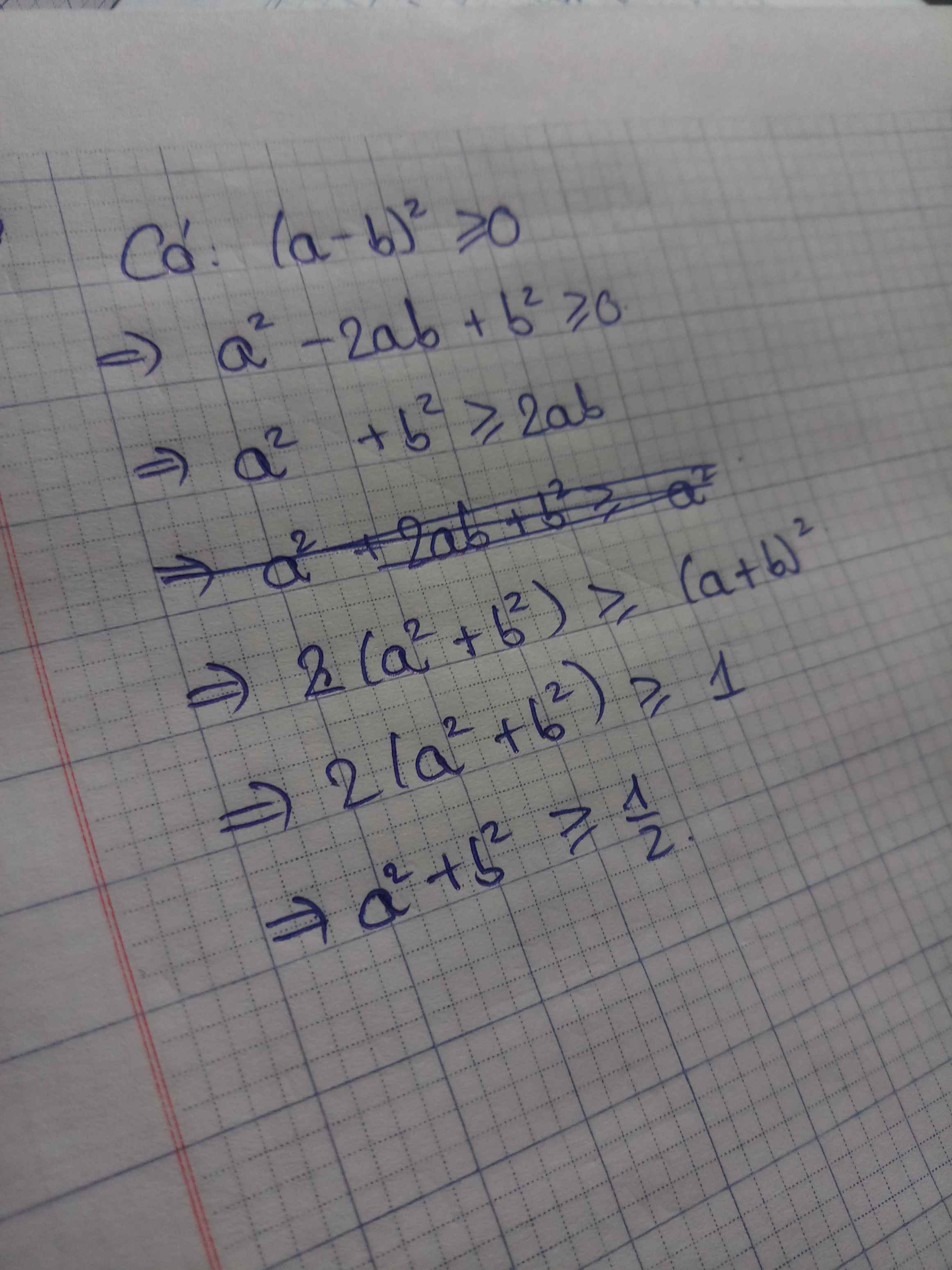1) chứng minh rằng nếu a;b;c là các số ko âm và b là số trung bình cộng của a và c thì ta có \(\frac{1}{\sqrt{a}+\sqrt{b}}+\frac{1}{\sqrt{b}+\sqrt{c}}=\frac{2}{\sqrt{c}+\sqrt{a}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) \(a^5-a=a\left(a^4-1\right)=a\left(a^2-1\right)\left(a^2+1\right)\)
\(=\left(a-1\right)a\left(a+1\right)\left(a^2-4+5\right)\)
\(=\left(a-1\right)a\left(a+1\right)\left(a^2-4\right)+5\left(a-1\right)a\left(a+1\right)\)
\(=\left(a-2\right)\left(a-1\right)a\left(a+1\right)\left(a+2\right)+5\left(a-1\right)a\left(a+1\right)⋮5\)
Vì \(\left(a-2\right)\left(a-1\right)a\left(a+1\right)\left(a+2\right)⋮5\)( tích 5 số nguyên liên tiếp chia hết cho 5)
và \(5\left(a-1\right)a\left(a+1\right)⋮5\)
=> \(a^5-a⋮5\)
Nếu \(a^5⋮5\)=> a chia hết cho 5

Bài 1:
a)
\(\overline{abcd}=100\overline{ab}+\overline{cd}\)
\(=100.2\overline{cd}+\overline{cd}\)
\(=201\overline{cd}\)
Mà \(201⋮67\)
\(\Rightarrow\overline{abcd}⋮67\)
b)
\(\overline{abc}=100\overline{a}+10\overline{b}+\overline{c}\)
\(=\left(100\overline{b}+10\overline{c}+\overline{a}\right)+\left(99\overline{a}-90\overline{b}-9\overline{c}\right)\)
\(=\overline{bca}+9\left[\left(12\overline{a}-9\overline{b}\right)-\left(\overline{a}+\overline{b}+\overline{c}\right)\right]\)
\(=\overline{bca}+27\left(4\overline{a}-3\overline{b}\right)-\left(\overline{a}+\overline{b}+\overline{c}\right)⋮27\)
\(\Rightarrow\overline{bca}-\left(\overline{a}+\overline{b}+\overline{c}\right)⋮27\)
\(\Rightarrow\left\{{}\begin{matrix}\overline{bca}⋮27\\\overline{a}+\overline{b}+\overline{c}⋮27\end{matrix}\right.\)
\(\Rightarrow\overline{bca}⋮27\)
Bài 2:
\(\overline{abcd}=\overline{ab}.100+\overline{cd}\)
\(=\overline{ab}.99+\overline{ab}+\overline{cd}\)
\(=\overline{ab}.11.99+\left(\overline{ab}+\overline{cd}\right)\)
Mà \(11⋮11\)
\(\Rightarrow\overline{ab}.11.9⋮11\)
\(\Rightarrow\overline{abcd}⋮11\).

mk cung dang mac bai nay nen mong nhieu bn giup do chi nha !


Ta có: a + b = 1 ⇔ b = 1 – a
Thay vào bất đẳng thức a2 + b2 ≥ 1/2 , ta được:
a2 + (1 – a)2 ≥ 1/2 ⇔ a2 + 1 – 2a + a2 ≥ 1/2
⇔ 2a2 – 2a + 1 ≥ 1/2 ⇔ 4a2 – 4a + 2 ≥ 1
⇔ 4a2 – 4a + 1 ≥ 0 ⇔ (2a – 1)2 ≥ 0 (luôn đúng)
Vậy bất đẳng thức được chứng minh

\(a+b=1=>b=1-a\)
\(=>a^2+\left(1-a\right)^2\ge\dfrac{1}{2}\)
\(=>a^2+1-2a+a^2\ge\dfrac{1}{2}\)
\(\Leftrightarrow-2a+2a^2+1\ge\dfrac{1}{2}\)
\(\Leftrightarrow\left(-2a+2a^2+1\right).2\ge1\)
\(\Leftrightarrow-4a+4a^2+2\ge1\)
\(\Leftrightarrow-4a+4a^2+1\ge0\)
\(\Leftrightarrow\left(2a-1\right)^2\ge0\left(đúng\right)\)
\(''=''\left(khi\right)2a-1=0=>a=\dfrac{1}{2}\)
Ta có: \(\left(a-b\right)^2\ge0\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow a^2+b^2+a^2+b^2\ge2ab+a^2+b^2\)
\(\Leftrightarrow2\left(a^2+b^2\right)\ge\left(a+b\right)^2\)
\(\Leftrightarrow2\left(a^2+b^2\right)\ge1\)
\(\Leftrightarrow a^2+b^2\ge\dfrac{1}{2}\left(đpcm\right)\)