Cho a,b,c là các số thực thỏa mãn
a(a2-3b2)=9;b(b2-3a2)=15
Tính giá trị của a2+b2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 7 2021
Bài 2 :
\(\left(a+b+c\right)^2=3\left(ab+bc+ca\right)\)
<=> a^2 + b^2 + c^2 + 2ab + 2bc + 2ca = 3ab + 3bc + 3ca
<=> a^2 + b^2 + c^2 = ab + bc + ca
<=> 2a^2 + 2b^2 + 2c^2 = 2ab + 2bc + 2ca
<=> ( a - b )^2 + ( b - c )^2 + ( c - a )^2 = 0
<=> a = b = c
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
1.
\(\Leftrightarrow2a^2+2b^2+18=2ab+6a+6b\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(a^2-6a+9\right)+\left(b^2-6b+9\right)=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(a-3\right)^2+\left(b-3\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-b=0\\a-3=0\\b-3=0\end{matrix}\right.\) \(\Leftrightarrow a=b=3\)
2.
\(\left(a+b+c\right)^2=3\left(ab+bc+ca\right)\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ca=3ab+3bc+3ca\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca=0\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-b=0\\b-c=0\\c-a=0\end{matrix}\right.\) \(\Leftrightarrow a=b=c\)
CM
26 tháng 11 2018
Chọn đáp án D
Ta có
Suy ra
Từ giả thiết ta có f ' x + f ' ' x = 10 e x
Để phương trình f ' x + f ' ' x = 10 e x có nghiệm
⇔ Phương trình (*) có nghiệm
* Nếu b = 0 thì S = a 2 ≥ 10
* Nếu b ≠ 0 thì S = a 2 - 2 a b + 3 b 2 ≥ 10 . a b 2 - 2 . a b + 3 a b 2 + 1 .
Đặt t = a b t ∈ R , suy ra S ≥ 10 . t 2 - 2 t + 3 t 2 + 1 .
Xét hàm số f t = t 2 - 2 t + 3 t 2 + 1 trên R.
Ta có
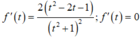
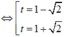
Bảng biến thiên:
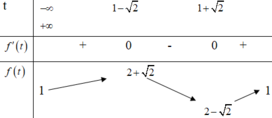
Quan sát bảng biến thiên ta thấy f t ≥ 2 - 2
TA
0
CM
4 tháng 7 2019
S = 2 ln a - ln b - ln c = ln a 2 b c = ln 1 = 0
do a 2 = b c
Chọn đáp án A.
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 2 2021
Đặt \(P=a^2+b^2+c^2+ab+bc+ca\)
\(P=\dfrac{1}{2}\left(a+b+c\right)^2+\dfrac{1}{2}\left(a^2+b^2+c^2\right)\)
\(P\ge\dfrac{1}{2}\left(a+b+c\right)^2+\dfrac{1}{6}\left(a+b+c\right)^2=6\)
Dấu "=" xảy ra khi \(a=b=c=1\)
