1,Cho đa thức:P(x)=x2+2mx+m2; Q(x)=x2+(2m+1)x+m2.Tìm m biết P(1)=Q(-1)
2,Biết \(2a^6b^2\)cùng dấu với \(-3a^5b^8\).So sánh A với 0
GIẢI RA GIÚP MK LUÔN
NHANH NHÉ!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.Mik làm rồi nhé!
\(b.P\left(x\right)+Q\left(x\right)=\left(2x^2-x+5\right)+\left(-2x^2+4x-1\right)\\ =2x^2-x+5-2x^2+4x-1\\ =3x+4\\ ------\\ P\left(x\right)-Q\left(x\right)=\left(2x^2-x+5\right)-\left(-2x^2+4x-1\right)\\ =2x^2-x+5+2x^2-4x+1\\ =4x^2-5x+6\)
\(c.\)nghiệm của đa thức P(x) + Q(x)
\(3x+4=0\\ \Leftrightarrow3x=-4\\ \Leftrightarrow x=\dfrac{-4}{3}\)
\(\Leftrightarrow\)vậy...

Chọn D
Đặt t= x-1 hay x= t+1, thay vào pt đã cho ta được pt:
t2+ 2(1-m) t+ m2- 3 m+2= 0 (2)
Để pt (1) có nghiệm x≤ 1 khi và chỉ khi pt (2) có nghiệm t≤ 0
TH1: Pt(2) có nghiệm : t1≤ 0 ≤ t2
Khi đó; P= t1.t2 ≤0 hay m2- 3m+ 2≤ 0 hay 1≤ m ≤ 2
TH2: pt (2) có nghiệm
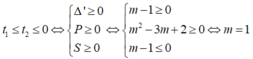
Kết luận: với 1≤ m≤ 2 thì pt (1) có nghiệm x≤1

Chọn D
Đặt t= x-1 hay x= t+1, thay vào pt đã cho ta được pt:
t2+ 2(1-m) t+ m2- 3 m+2= 0 (2)
Để pt (1) có nghiệm x ≥ 1 khi và chi khi pt (2) có nghiệm t ≥ 0
+ TH1: Pt (2) có nghiệm t1 ≤ 0 ≤ t2
Khi đó; P= t1.t2 ≤ 0 hay m2- 3m+ 2 ≤ 0
Từ đó; 1≤ m≤ 2
+ TH2: Pt (2) có nghiệm :
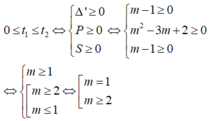
Kết luận: với ![]() thì pt (1) có nghiệm x ≥ 1
thì pt (1) có nghiệm x ≥ 1

Bạn nên tách lẻ từng bài ra để được hỗ trợ tốt hơn, không nên đăng 1 loạt bài như thế này nhé.
2:
a: P(x)=3x^2-4x-1
Q(x)=-3x^2-4x-2
b:F(x)=-3x^2-4x-2-3x^2+4x+1=-6x^2-1
Q(x)=3x^2-4x-1+3x^2+4x+2=6x^2+1
c: F(-2)=-6*4-1=-25
Q(3)=-27-12-2=-41

Chọn C
Đặt t= x-1 hay x= t+1, thay vào pt đã cho ta được pt:
t2+ 2(1-m) t+ m2- 3 m+2= 0 (2)
pt (1) có 2 nghiệm thỏa mãn x1< 1< x2 khi và chỉ khi pt (2) có 2 nghiệm: t1< 0 < t2 suy ra P < 0
Hay m2- 3m+ 2 < 0
Do đó: 1 < m < 2
Kết luận: với 1< m< 2 thì pt (1) có hai nghiệm x1< 1< x2

Chọn D
Đặt t= x-1 hay x= t+1, thay vào pt đã cho ta được pt:
t2+ 2(1-m) t+ m2- 3 m+2= 0 (2)
pt (1) có 2 nghiệm thỏa x1< x2< 1 khi và chỉ khi pt (2) có 2 nghiệm:
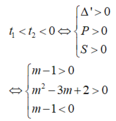
(vô nghiệm)
Kết luận: không tồn tại m thỏa mãn bài toán.