Trên đường thẳng xy lấy 4 điểm A;B;C;D sao cho AB=6 cm và C là trung điểm của AB ; D là trung điểm của CB. Lấy thêm 1 số điểm phân biệt trên đường thẳng xy không trùng với 4 điểm A,B,C,D.Qua 2 điểm vẽ được 1 đoạn thẳng và đếm được tất cả 351 đoạn thẳng. Hỏi đã lấy thêm mấy điểm phân biệt trên đường thẳng xy?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a ) Vì C là trung điểm của AB
=> BC = AB / 2 = 6 / 2 = 3 cm
Vì D là trung điểm của BC
=> CD = BC / 2 = 3 / 2 = 1,5 cm
Vì AC và AD là 2 tia đối nhau
nên C nằm giữa A và D
=> AC + CD = AD
=> AD = 3 +1,5 = 4,5 cm
Vậy AD = 4,5 cm
Nếu bạn thấy chỗ nào chx hiểu để mình làm lại cho dễ hiểu hơn

Để có 456 đoạn thẳng thì cần thêm n đường
Theo đề, ta có: (n+4)(n+3)=456
=>n^2+7n+12=456
=>n^2+7n-444=0
=>\(n\in\varnothing\)

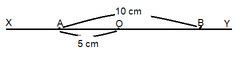
a. điểm O nằm giữa 2 điểm còn lại
b. ta có : OA + OB = AB
hay 5 + OB = 10
OB = 10 - 5 = 5(cm)
c. vì \(OA=OB=\dfrac{AB}{2}=5\left(cm\right)\)
nên O là trung điểm AB

a: OA<OB
=>A nằm giữa O và B
=>AB=4-3=1cm
b: Số đoạn thẳng là \(C^2_{200}=19900\left(đoạn\right)\)

a. Hai tia đối nhau gốc O là tia Ox(hoặc OA) và tia Oy.
b. Hai tia Ox và tia Ax không trùng nhau vì hai tia đó không có chung điểm gốc.
c. Trên đường thẳng xy, lấy thêm 2019 điểm không trùng nhau với điểm O và A thì sẽ có 2019 + 2 = 2021 điểm trên đường thẳng xy. 2021 điểm đó sẽ tạo ra 2020 đoạn thẳng nhưng 2 điểm ở ngoài cùng sẽ tạo ra tia nên trên sẽ có 2020 - 2 = 2018 đoạn thẳng( nếu không tính các đoạn thẳng trùng nhau
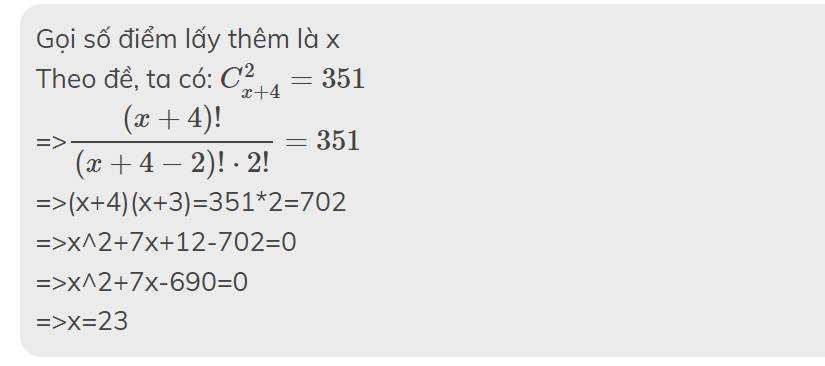
Gọi số điểm lấy thêm là x
Theo đề, ta có: \(C^2_{x+4}=351\)
=>\(\dfrac{\left(x+4\right)!}{\left(x+4-2\right)!\cdot2!}=351\)
=>(x+4)(x+3)=351*2=702
=>x^2+7x+12-702=0
=>x^2+7x-690=0
=>x=23