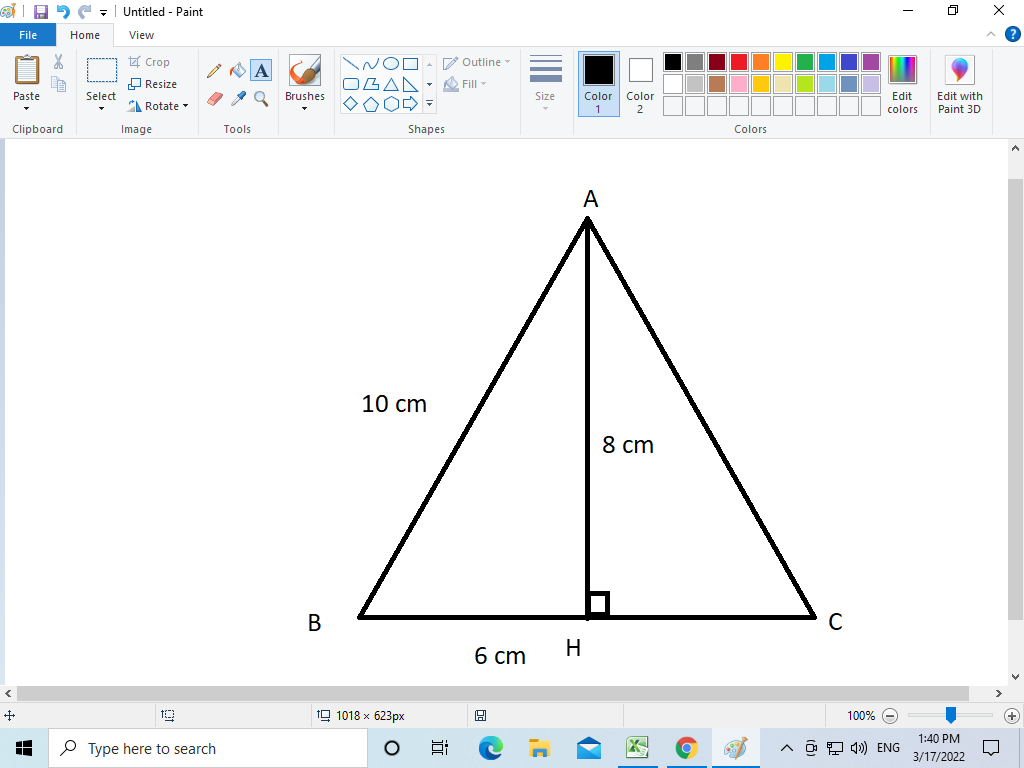
Cho tam giác ABC cân tại A vẽ AH vuông góc với BC tại H.Biết AB=10cm;BH==6cm
a)tính AH
b)tam giác ABD = tam giác ACH
c) trên BA lấy D,CA lấy E sao cho BD = CE . Chứng minh tam giác HDE cân
d) Chứng minh AH là trung trực của DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 2 2022
a: AH=8cm
b: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
c: Xét ΔDBH và ΔECH
DB=EC
\(\widehat{B}=\widehat{C}\)
BH=CH
Do đó: ΔDBH=ΔECH
Suy ra: HD=HE
hay ΔHDE cân tại H
d: Ta có: AD=AE
nên A nằm trên đường trung trực của DE(1)
Ta có: HD=HE
nên H nằm trên đường trung trực của DE(2)
Từ (1) và (2) suy ra AH là đường trung trực của DE
17 tháng 3 2022
\(\text{Xét }\Delta ABC\text{ có:}\)
\(AB>AH>BH\left(10cm>8cm>6cm\right)\)
\(\widehat{H}>\widehat{B}>\widehat{A\text{(quan hệ giữa cạnh và góc đối diện trong tam giác)}}\)
7 tháng 9 2021
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
Suy ra: BH=CH
b: Ta có: BH=CH
nên \(BH=CH=\dfrac{BC}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Xét ΔAHB vuông tại H có
\(AB^2=AH^2+HB^2\)
hay AH=12(cm)
\(\Leftrightarrow AG=8\left(cm\right)\)
7 tháng 9 2021
c: Xét ΔABC có
N là trung điểm của AB
M là trung điểm của AC
Do đó: NM là đường trung bình của ΔABC
Suy ra: NM//BC
CD
17 tháng 3 2020
a, AH= 8cm
vi ad la tia p/g cua bc => a1=a2
xet tg abh va tg ach co
ab=ac(gt) }
a1=a2 (gt) } gt ABH =TG ACH (C.GC)
ah canh chung }
c,vì abh = ach câu b =>hde cân
17 tháng 3 2016
a) xét tg HAB và tg HAC có AB=AC(gt);góc AHB=góc AHC(=90 độ),chung AH
=>tg HAB và tg HAC bằng nhau (c.g.c)
b)=>HB=HC =>H là tđ BC. ta có tg ABH vuông tại H
=>AB^2=BH^2+AH^2 ( do H là tđ BC(cmt) vàBC=16cm(gt))+định lí pytago
hay 10^2=8^2+AH^2
AH^2=36
=> AH=6
c)có tg hab=tg hac=>bah=cah
xét tg eah và tg fah có: chung ah
bah=cah(cmt)
aeh=afh
=>tg eah=tg fah =>af=ae.MÀ ab=ac(gt)=>fc=be
=>tg hbe=tg hcf(c.g.c)
d)cmt.có af=fe(cmt)=>tgaef cân
k dúng mình cái mình làm bài này mệt lắm r
a, Xét tam giác HBA vuông tại H có:
AB2=AH2+BH2(định lí py ta go)
hay 100=AH2+36
=> AH2=64
=> AH=8(cm)
b, Xét tam giác ABH và tam giác ACH có:
góc AHB=góc AHC =90 độ
AB=AC (tam giác ABC cân tại A)
AH chung
=> tam giác ABH = tam giác ACH
c,
Xét tam giác DBH và tam giác ECH có:
BD=CE (gt)
góc DBH= góc ECH (tam giác ABC Cân tại A)
BH=CH (trong tam giác cân, đường cao đồng thời là đường trung tuyến)
=> tam giác DBH=tam giác ECH
=> DH=EH( 2 cạnh tương ứng)
=> tam giác HDE cân tại H
d) Vì AB = AC; BD = CE
mà AB - BD = AD
AC - CE = AE
=> AD = AE
Vì ΔHDE cân
=> H ∈ đường trung trực cạnh DE (1)
Xét ΔADHvàΔAEHcó
AD = AE (cmt)
AH (chung)
DH = HE (cmt)
Do đó: ΔADH=ΔAEH(c−c−c)
=> AD = AE ( hai cạnh tương ứng)
=> ΔADE cân tại A
=> A ∈ đường trung trực cạnh DE (2)
(1); (2) => A,H ∈ đường trung trực cạnh DE
=>AH là đường trung trực cạnh DE
CHÚC BẠN HỌC TỐT
bn j đó ơi cảm ơn bn đx giải cho mk nhung phần b) sai rồi nha