Cho tam giác ABC vuông góc tại A có AB=5cm;AC=7cm,vẽ phân giác AD;phân giác ngoài Ax. Hạ BE vuông góc AD; CF vuông góc AD; FI vuông góc EC; FI cắt Ax tại K
a) Tính BC
b) Chứng minh tam giác ABE; tam giác AFC là tam giác vuông cân
c) Chứng minh AK=EF
Các bạn giúp mình với mình xin cảm ơn

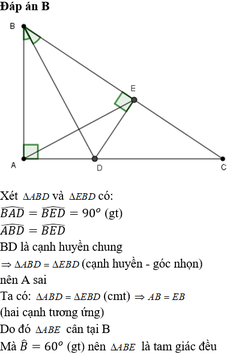
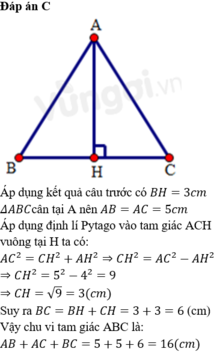
a) BC^2= Ac^2+Ab^2=> Bc^2=74=> Bc=căn 74. b)vì Ad là phân giác nên góc BAE và góc FAC bằng 45. Hai tam giác ABE và AFC đều vuông và đều có 1 góc 45 nên => tam giác vuông cân. Câu c) AD vuông góc Ax ( hai tia phân giác trong và phan giác ngoài của cùng 1 góc thì vuông góc nhau). Xét 2 tam giác vuông FAK và FEC có. FA=FC( theo câu b). Góc FCE = AFK cùng phụ FEC( do Tg FEI vuôg tại I). Và FAK=EFC=90 => tg AFK=tgEFC(g.c.g)=> AK=EF. phiền bạn tự trình bày lại cho hợp lí. Chúc bạn học tốt
cảm ơn bạn đã đã giải giúp mình