Có bao nhiêu giá trị nguyên của m thuộc khoảng (−8;8) để hàm số y = 2 9 - x 2 9 - x 2 - m đồng biến trên khoảng 0 ; 5 ?
A. 9
B. 7
C. 8
D. 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B.
Ta có yêu cầu bài toán tương đương với
y ' = m x 9 - x 2 ( 9 - x 2 - m ) 2 > 0 , ∀ x ∈ 0 ; 5
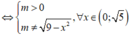
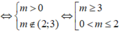
![]()
Vậy có tất cả 7 số nguyên thoả mãn.

TH1 : Đồ thị hàm số y = 3mx2 - (m - 9)x + 8 - m2 có hai điểm phân biệt đối xứng nhau qua gốc tọa độ khi hàm số trên là hàm số lẻ trên tập xác định R
Khi đó f(x) + f(-x) = 0
⇒ 3mx2 + 3mx2 - (m - 9)x + 8- m2 + (m - 9)x - m2 + 8 = 0
⇒ 6mx2 + 16 = 0 (không có m)

Chọn B
Phương pháp:
Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.
Ta sử dụng phương trình ![]() có hai nghiệm dương phân biệt
có hai nghiệm dương phân biệt
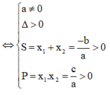
Cách giải:
Ta có ![]()
Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.
Khi đó
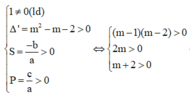
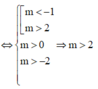
Mà ![]()
![]() nên có 2018 – 3 + 1 = 2016 giá trị m thỏa mãn.
nên có 2018 – 3 + 1 = 2016 giá trị m thỏa mãn.

Ta có:
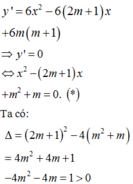
⇒ * luôn có hai nghiệm phân biệt x 1 ; x 2 x 1 < x 2 với mọi m.
Áp dụng hệ thức Vi-ét ta có:
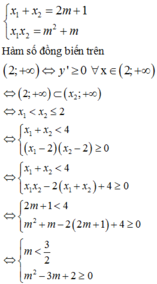
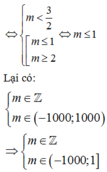
Vậy có tất cả 1001 giá trị m thỏa mãn bài toán.
Chọn B.
Ta có yêu cầu bài toán tương đương với:
Vậy có tất cả 7 số nguyên thoả mãn.
Chọn đáp án B.