Câu 9:
Cho đường tròn (O;6cm) và điểm A nằm trên đường tròn.Qua A kẻ tiếp tuyến Ax
trên Ax lấy điểm B sao cho OB=10 cm.Khi đó AB= ???
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 5 2023
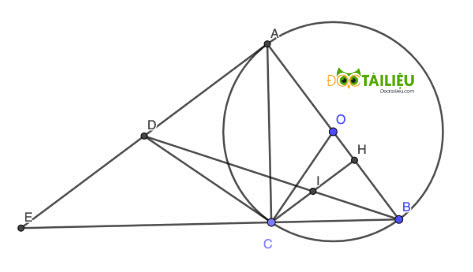
DA,DC là tiếp tuyến của (O)
=>DA=DC
=>OD vuông góc AC
CH vuông góc AB
=>AD//CH
=>CI/AD=IM/MD
IH/AD=BI/BD
mà IM/MD=BI/BD
nên CI/AD=IH/AD
=>CI=IH
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2023
Ta có: \(OB=OC=R\) ; \(AB=AC\) (t/c hai tiếp tuyến cắt nhau)
\(\Rightarrow OA\) là trung trực của BC
\(\Rightarrow OA\) là phân giác góc \(\widehat{BAC}\) (1)
Mặt khác I thuộc OA \(\Rightarrow IB=IC\Rightarrow\Delta IBC\) cân tại I
\(\Rightarrow\widehat{CBI}=\widehat{BCI}\)
Mà \(\widehat{BCI}=\widehat{ABI}\) (góc nội tiếp và góc tiếp tuyến cùng chắn cung BI)
\(\Rightarrow\widehat{CBI}=\widehat{ABI}\Rightarrow BI\) là phân giác \(\widehat{ABC}\) (2)
(1);(2) \(\Rightarrow I\) là tâm đường tròn nội tiếp tam giác ABC
7 tháng 1 2021
a) Xét ΔOAB có OA=OB(=R)
nên ΔOAB cân tại O(Định nghĩa tam giác cân)
Ta có: ΔOAB cân tại O(cmt)
mà OC là đường cao ứng với cạnh đáy AB(OH⊥AB, C∈OH)
nên OC là đường phân giác ứng với cạnh AB(Định lí tam giác cân)
⇒\(\widehat{AOC}=\widehat{BOC}\)
Xét ΔAOC và ΔBOC có
OA=OB(=R)
\(\widehat{AOC}=\widehat{BOC}\)(cmt)
OC chung
Do đó: ΔAOC=ΔBOC(c-g-c)
⇒\(\widehat{OAC}=\widehat{OBC}\)(hai góc tương ứng)
mà \(\widehat{OAC}=90^0\)(CA là tiếp tuyến của (O) có A là tiếp điểm)
nên \(\widehat{OBC}=90^0\)
hay CB⊥OB tại B
Xét (O) có
OB là bán kính
CB⊥OB tại B(cmt)
Do đó: CB là tiếp tuyến của (O)(Dấu hiệu nhận biết tiếp tuyến đường tròn)
b) Xét (O) có
OH là một phần đường kính
AB là dây
OH⊥AB tại H(gt)
Do đó: H là trung điểm của AB(Định lí đường kính vuông góc với dây)
⇒\(BH=\dfrac{AB}{2}=\dfrac{24}{2}=12cm\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔOBC vuông tại B có BH là đường cao ứng với cạnh huyền OC, ta được:
\(\dfrac{1}{BH^2}=\dfrac{1}{BC^2}+\dfrac{1}{BO^2}\)
\(\Leftrightarrow\dfrac{1}{12^2}=\dfrac{1}{BC^2}+\dfrac{1}{20^2}\)
\(\Leftrightarrow\dfrac{1}{BC^2}=\dfrac{1}{12^2}-\dfrac{1}{20^2}=\dfrac{1}{144}-\dfrac{1}{400}=\dfrac{1}{225}\)
\(\Leftrightarrow BC^2=225\)
hay BC=15(cm)
Áp dụng định lí Pytago vào ΔOBC vuông tại B, ta được:
\(OC^2=OB^2+BC^2\)
\(\Leftrightarrow OC^2=15^2+20^2=625\)
hay OC=25(cm)
Vậy: OC=25cm
