Cho hàm số y=f(x)liên tục trên đoạn [1;5]và f(1)=2,f(5)=10. Khẳng định nào sau đây đúng?
A. Phương trình ![]() vô nghiệm.
vô nghiệm.
B. Phương trình ![]() có ít nhất một nghiệm trên khoảng
có ít nhất một nghiệm trên khoảng ![]() .
.
C. Phương trình ![]() có hai nghiệm
có hai nghiệm ![]() .
.
D. Phương trình ![]() vô nghiệm.
vô nghiệm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có
![]()
![]()
![]()
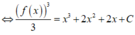
![]()
Ta có: f ( 0 ) = 1 ⇒ 1 = 3 C
![]()
![]()
Xét hàm ![]() trên [-2;1]
trên [-2;1]
Ta có
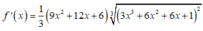
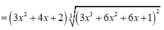
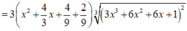
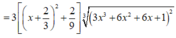
Nhận thấy f ' ( x ) > 0 ∀ x ∈ ℝ ⇒ Hàm số đồng biến trên (-2;1)
Suy ra m a x - 2 ; 1 f ( x ) = f ( 1 ) = 16 3
Chọn đáp án C.

Phương pháp: Sử dụng phương pháp đổi biến, đặt t = u(x)
Cách giải:
Đặt
![]()
Đổi cận 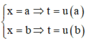
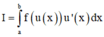


![]()
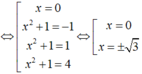
Các nghiệm trên đều là các nghiệm bội lẻ, do đó đều là cực trị của hàm số ![]()
Xét x = -1 ta có ![]()
từ đó ta có bảng xét dấu g’(x) như sau:
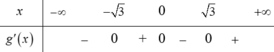
Dựa vào các đáp án ta thấy hàm số y = g(x) nghịch biến trên (0;1)
Chọn B

Chọn A.
Ta có ∫ 1 4 f ' ( x ) d x = f ( 4 ) - f ( 1 ) ⇒ f ( 4 ) = f ( 1 ) + 17 = 29
Chọn B
Đặt .
.
Vì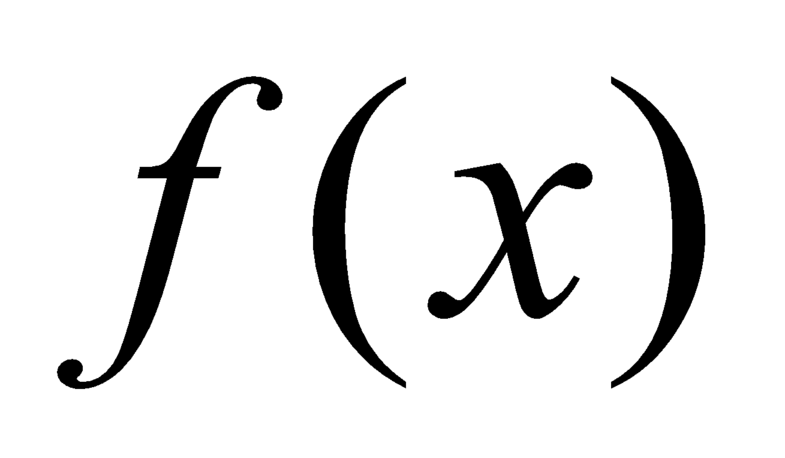 liên tục trên đoạn
liên tục trên đoạn 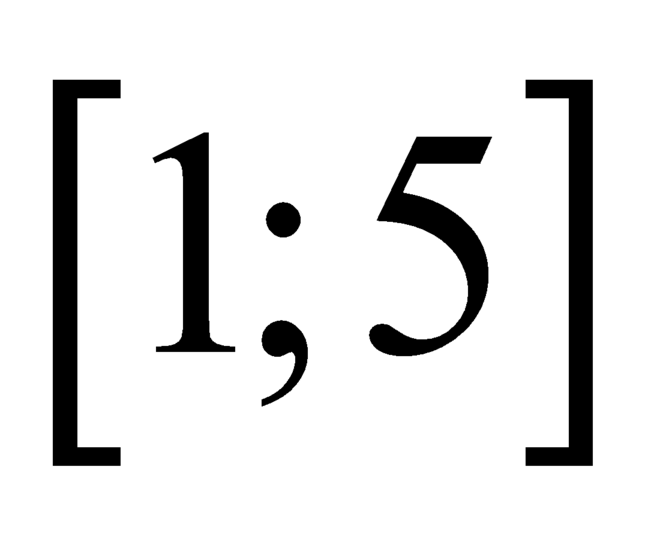 nên
nên 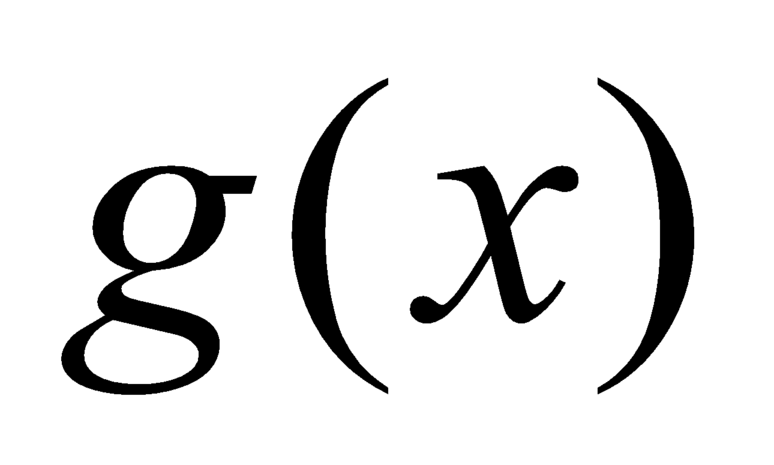 liên tục trên
liên tục trên 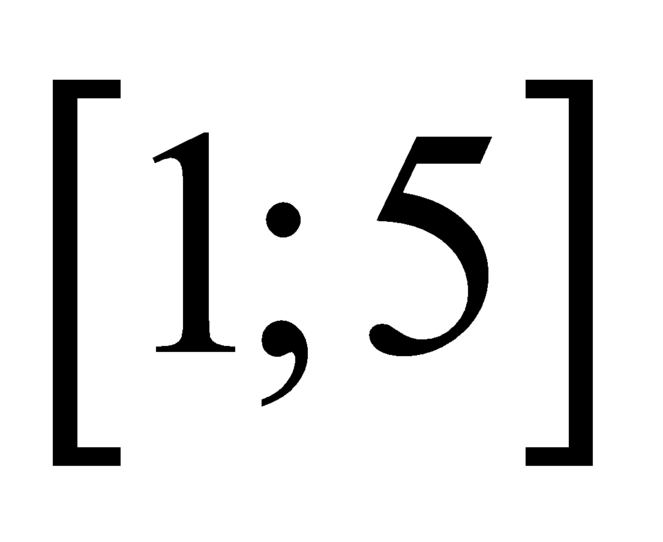 .Ta xét các trường hợp sau:
.Ta xét các trường hợp sau:
+ Với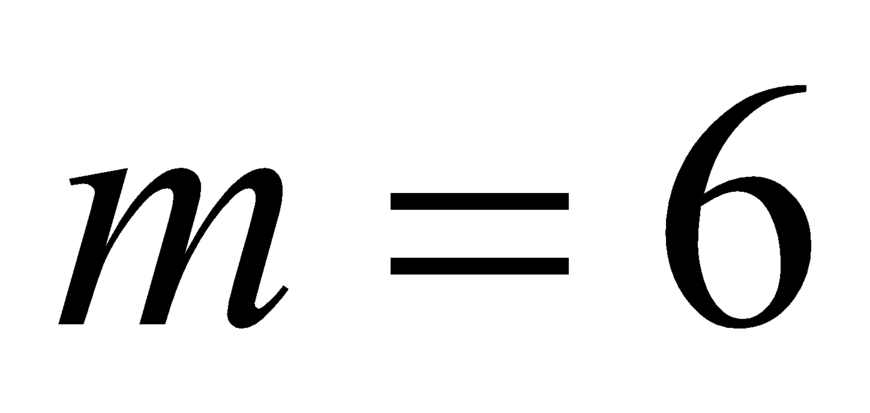
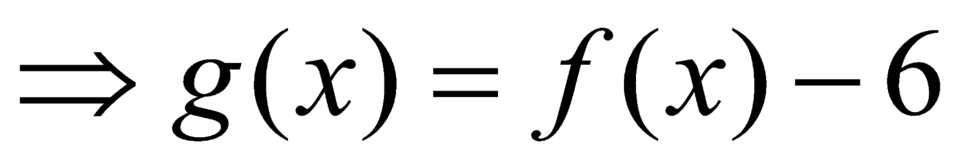 .
.
Ta có: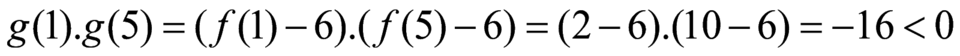 .
.
Suy ra phương trình có ít nhất một nghiệm trên khoảng
có ít nhất một nghiệm trên khoảng 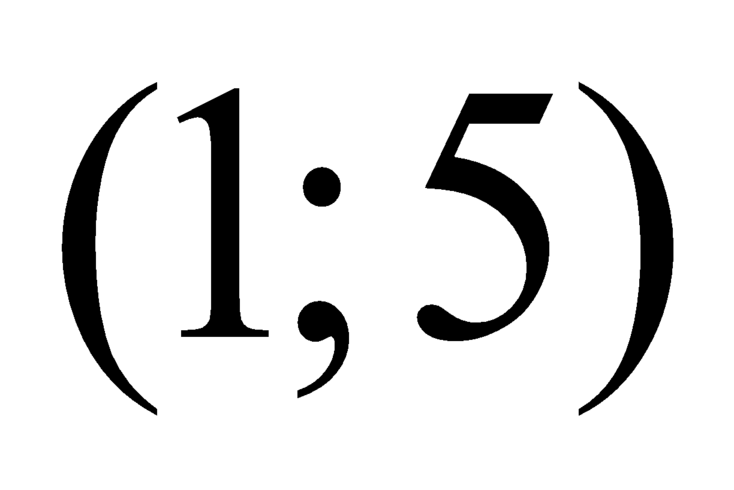 .
.
Vậy A sai.
+ Với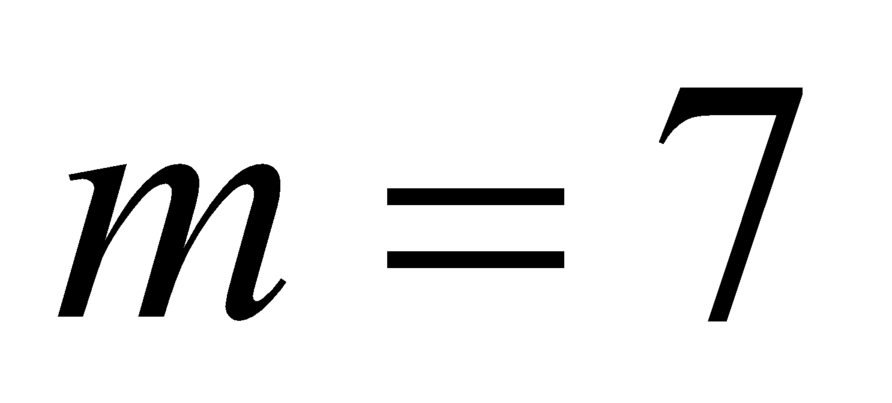
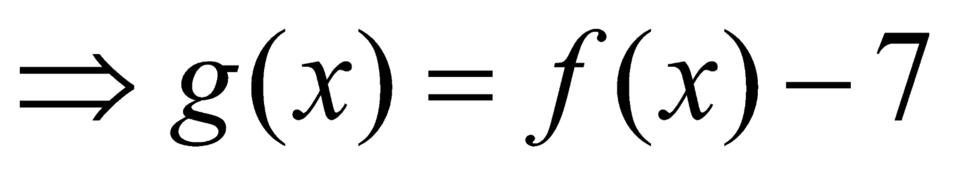 .
.
Ta có: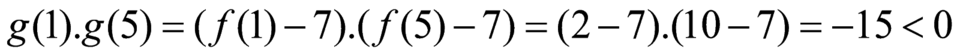 .
.
Suy ra phương trình có ít nhất một nghiệm trên khoảng
có ít nhất một nghiệm trên khoảng 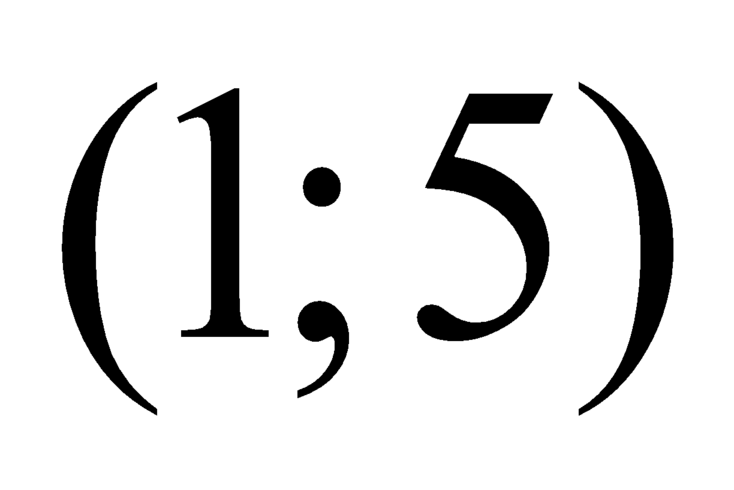 .
.
Vậy B đúng, D sai.
+ Với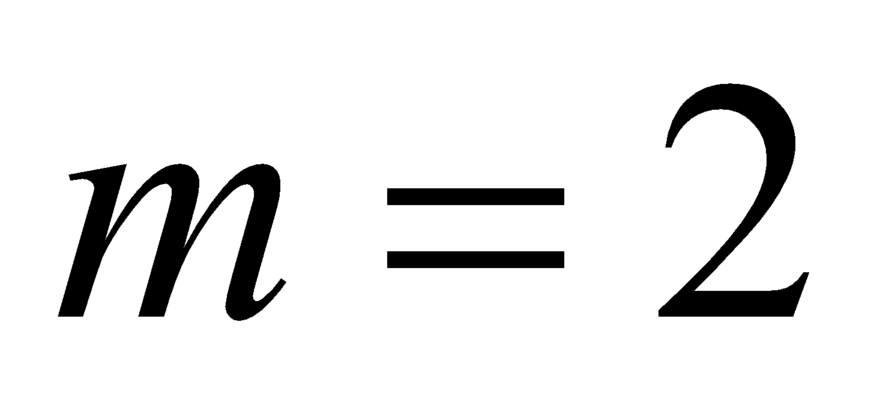
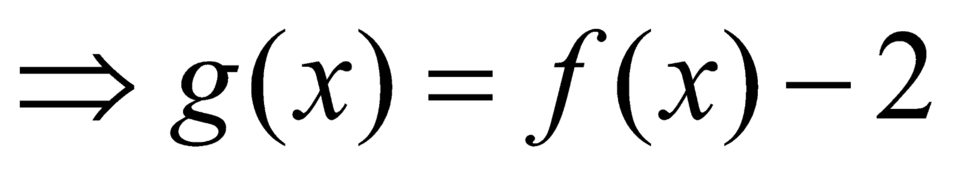 .
.
Ta có: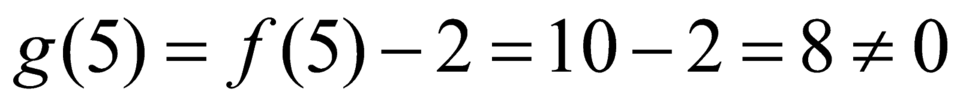 Suy ra
Suy ra 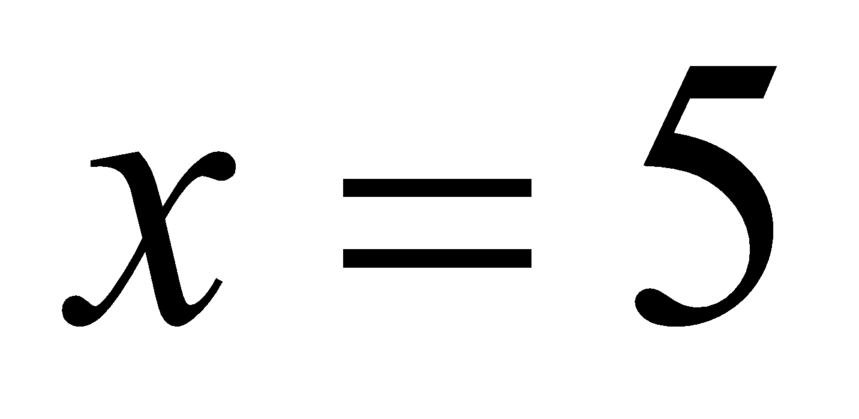 không là nghiệm của phương trình
không là nghiệm của phương trình 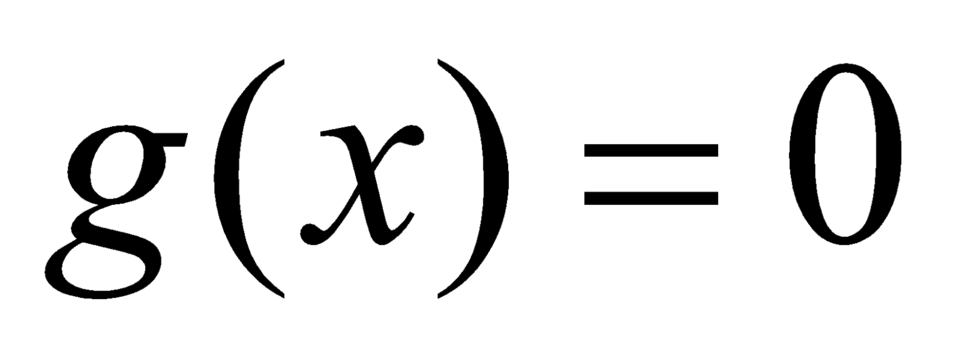 hay
hay 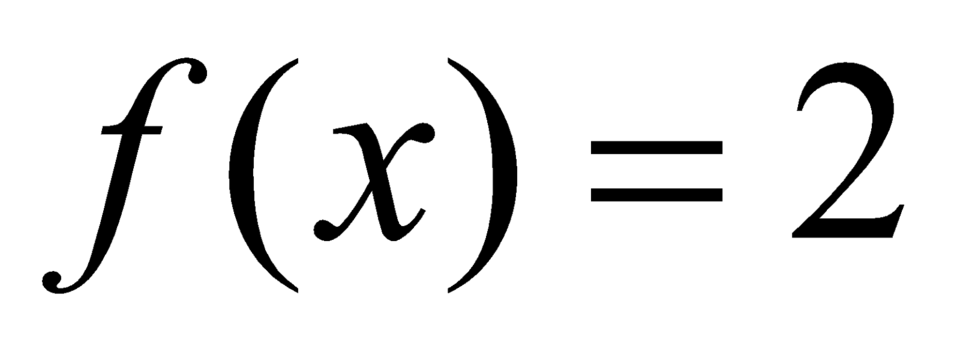 .
.
Vậy C sai.