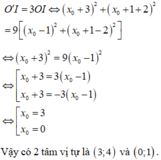Cho đường tròn (0;4cm) đường kính AB. Lấy điểm H thuộc AO sao cho OH=1cm. Kẻ dây cung DC vuông góc với AB tại H
a. chứng minh tam giác ABC vuông và tính độ dài AC
b. tiếp tuyến tại A của (O) cắt BC tại E. chứng minh tam giác CBD cân và EC/DH=EA/DB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 10 2019
Đáp án C
(C) có tâm I(0;1) bán kính 2
Đox: I(0;1) -> I’( 0;–1)
Phương trình đường tròn (C’): x 2 + y 2 + 2 y − 3 = 0
CM
15 tháng 3 2017
Đáp án A
Đường tròn C có tâm K 1 ; 2 , bán kính R = 1 + 4 − 4 = 1 .
Đường tròn C ' có tâm K ' − 3 ; − 2 , bán kính R ' = 9 + 4 − 4 = 3.
Giả sử V 1 ; k C = C '
khi đó k = R ' R ⇒ k = 3 ⇔ k = ± 3
Với k = 3 ⇒ I K ' → = 3 I K → ⇒ − 3 − x 1 = 3 1 − x 1 − 2 − y 1 = 3 2 − y 1 ⇒ I 3 ; 4
Với k = − 3 ⇒ I K ' → = − 3 I K → ⇒ − 3 − x 1 = − 3 1 − x 1 − 2 − y 1 = − 3 2 − y 1 ⇒ I 0 ; 1
CM
3 tháng 9 2017
(C): x 2 + y 2 − 4 x + 2 y − 15 = 0 và đường thẳng ∆: - 4x + 3y + 1 = 0.
Đường tròn (C): x 2 + y 2 − 4 x + 2 y − 15 = 0 có tâm I(2; -1) và bán kính R = 20 .
Khoảng cách d I , ∆ = − 4.2 + 3. − 1 + 1 5 = 2 < R nên đường thẳng cắt đường tròn tại hai điểm phân biệt A, B cách nhau một khoảng là
A B = 2 R 2 − d I , ∆ 2 = 8 .
ĐÁP ÁN C
CM
20 tháng 5 2019
Đường tròn (C): x 2 + y 2 + 4 x − 4 y − 10 = 0 có tâm I(-2;2) và bán kính R = 3 2 .
Khoảng cách d ( I ; Δ ) = − 2 + 2 + m 1 2 + 1 2 = m 2
Để đường thẳng tiếp xúc đường tròn thì:
d ( I ; Δ ) = R ⇔ m 2 = 3 2 ⇔ m = 6 ⇔ m = ± 6
ĐÁP ÁN A
8 tháng 1 2022
a: Xét (O) có
SA là tiếp tuyến
nên SA vuông góc với OA
hay ΔOAS vuông tại A
b: Xét ΔOAS và ΔOBS có
OA=OB
\(\widehat{SOA}=\widehat{SOB}\)
OS chung
Do đó: ΔOAS=ΔOBS
Suy ra: \(\widehat{OAS}=\widehat{OBS}=90^0\)
hay SB là tiếp tuyến của (O)
