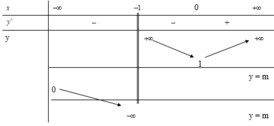
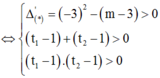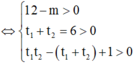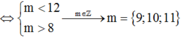Có bao nhiêu giá trị m nguyên với m ∈ [ - 4 ; 4 ] để phương trình e x = m ( x + 1 ) có một nghiệm duy nhất?
A. 4.
B. 5.
C. 6.
D. 7.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Đáp án C
Đặt t = log 2 x với x ∈ 0 ; + ∞ thì t ∈ ℝ , khi đó bất phương trình trở thành t 2 + m t - m > 0 *
Để (*) nghiệm đúng với mọi t ∈ ℝ ⇔ ∆ * ≤ 0 ⇔ m 2 + 4 m ≤ 0 ⇔ m ∈ - 4 ; 0
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện

3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)

Lời giải:
Để $(m^2-4)x=m(m-2)$ có nghiệm duy nhất thì $m^2-4\neq 0$
$\Leftrightarrow (m-2)(m+2)\neq 0$
$\Leftrightarrow m\neq \pm 2$
Mà $m$ nguyên và $m\in [-5;5]$ nên $m\in\left\{-5; -4; -3; -1; 0; 1;3;4;5\right\}$

Chọn D.
Đặt ![]() khi đó phương trình tương đương với: t2 - 6t + m – 3 = 0 (*)
khi đó phương trình tương đương với: t2 - 6t + m – 3 = 0 (*)
Để phương trình đã cho có 4 nghiệm phân biệt khi (*) có 2 nghiệm dương phân biệt lớn hơn 1.