1) Cho hai hàm số y = f (x) và y = h (x) được xác định bởi công thức f (x) = [x] và h (x) = {x}.
Tính h(x) biết x∈{−4,2;−3,24;−1,15;−0,2;0,2;1,15;3,24;4,2}.
2) Hàm số y = f (x) được xác định như sau: Ứng với mỗi số tự nhiên có ba chữ số f(x) bằng tổng các chữ số của số đã cho.
Tính f (212).

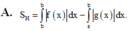
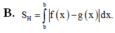
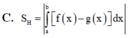
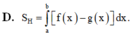


f (x) = [x] = phần nguyên của x : là số nguyên lớn nhất nhỏ hơn x
h(x) = {x} = x - [x] = phần lẻ của x
1) x = -4,2 => [x] = -5 => h(-4,2) = {-4,2} = -4,2 - (-5) = 0,8
các số còn lại tương tự
[ x] là phần nguyên của x