Cho hàm số f (x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;3] thoả mãn f(0)=2,f(3)=8 và ∫ 0 3 ( f ' ( x ) ) 2 f ( x ) d x = 8 3 . Tính f(2).
A. 50/9.
B. 49/9.
C. 47/9.
D. 52/9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
26 tháng 10 2017
Đúng(0)
Những câu hỏi liên quan
CM
23 tháng 10 2017
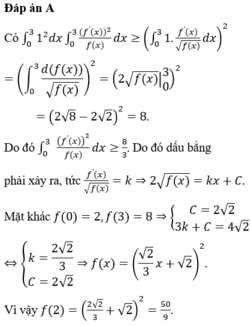
Theo bất đẳng thức Cauchy-Schwarz cho tích phân có:
Đáp án A
CM
22 tháng 3 2017
Đặt g ( x ) = log 2 ( f ( 2 x ) ) ,
ta có g ' ( x ) = 2 f ' ( 2 x ) f ( 2 x ) ln 2
Theo giả thiết, ta có f ( 2 x ) > 0 , ∀ x ∈ ℝ
Do đó
g ' ( x ) ≥ 0 ⇔ f ' ( 2 x ) ≥ 0 ⇔ [ - 1 ≤ 2 x ≤ 1 2 x ≥ 2 ⇔ [ - 1 2 ≤ x ≤ 1 2 x ≥ 1
(dấu bằng xảy ra tại hữu hạn điểm). Suy ra hàm số y=g(x) đồng biến trên các khoảng - 1 2 ; 1 2 và 1 ; + ∞ . Chọn A.
Chọn đáp án A.
