Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C.
Phương pháp: Lập hệ phương trình tìm a,b,c.
Cách giải: Từ giả thiết ta có hệ:
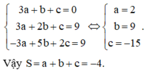
Đáp án D
Nếu hai mặt phẳng (P) và (Q) song song với nhau và M thuộc mặt phẳng (P) thì:
+ Khoảng cách từ điểm M đến mặt phẳng (Q) không phụ thuộc vào M.
+ Khoảng cách giữa hai mặt phẳng (P) và (Q) chính là khoảng cách từ M đến mặt phẳng (Q)
+ Khoảng cách giữa hai mặt phẳng (P) và (Q) là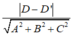 
+ Đặc biệt, khoảng cách giữa hai mặt phẳng (P) và (Q) là |D - D'| khi và chỉ khi:
A 2 + B 2 + C 2 =1
Do đó, mệnh đề D có thể sai.
Đáp án C.
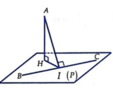
Ta có B C → = - 2 ; - 1 ; - 2 nên phương trình đường thẳng BC là x = 1 - 2 t y = - t ( t ∈ ℝ ) z = 2 - 2 t .
Gọi I là hình chiếu vuông góc của A trên BC, H là hình chiếu vuông góc của A trên mặt phẳng (P) . Khi đó A H = d A ; P ≤ A I và AH đạt giá trị lớn nhất khi H ≡ I . Suy ra mặt phẳng (P) qua I và vuông góc với AI.
Từ I ∈ B C ⇒ I 1 - 2 t ; - t ; 2 - 2 t và A I → = - 1 - 2 t ; - t - 5 ; - 1 - 2 t .
Lại có A I ⊥ B C ⇔ A I → . B C → = 0 ⇔ 2 ( 1 + 2 t ) + ( t + 5 ) + 2 ( 1 + 2 t ) = 0 ⇔ t = - 1 .
Mặt phẳng (P) đi qua I(3;1;4) và nhận VTPT là A I → = 1 ; - 4 ; 1 nên có phương trình tổng quát là: x - 4 y + z - 3 = 0 .
Vậy a = 1 , b = - 4 , c = 1 , d = - 3 → M = 1 + 1 - 4 - 3 = - 2 7 .
Chọn D