Question

[Ánh Dương]

Có bao nhiêu giá trị nguyên của m\(\in\)(-20;20) để hàm số \(y=\frac{2x+m}{2x^4+7x^3-\left(3m-4\right)x^2-\left(5m+4\right)x+m^2+2m}\)có tập xác định là R

Answer 1

[Nguyễn Việt Lâm]

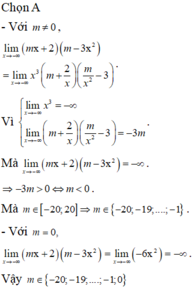
Để hàm xác định trên R

\(\Leftrightarrow2x^4+7x^2-\left(3m-4\right)x^2-\left(5m+4\right)x+m^2+2m=0\) vô nghiệm

\(\Leftrightarrow\left(x^2+2x-m\right)\left(2x^2+3x-m-2\right)=0\) vô nghiệm

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta_1'=1+m< 0\\\Delta_2=9-8\left(-m-2\right)< 0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m< -1\\m< -\frac{25}{8}\end{matrix}\right.\) \(\Rightarrow-20< m< -\frac{25}{8}\)

Vậy \(m=\left\{-19;-18;...;-4\right\}\) có 16 giá trị nguyên

Answer 2

[Ánh Dương]

nếu tập xác định chỉ là 1 khoảng trên trục số thì sao ạ?