Xét x,y là các số thực thuộc đoạn [1;2]. Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức S = x y + y x . Tính M + m
A. 5 2
B. 4
C. 9 2
D. 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
14 tháng 9 2019
Đúng(0)
Những câu hỏi liên quan
NV
1
7 tháng 10 2021
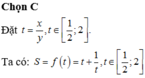
Ta có:
Đặt \(A=x+y+\dfrac{1}{x}+\dfrac{1}{y}\)
\(\Leftrightarrow A=x+y+\dfrac{4}{4x}+\dfrac{4}{4y}\)
\(\Leftrightarrow A=x+y+\dfrac{1}{4x}+\dfrac{3}{4x}+\dfrac{1}{4y}+\dfrac{3}{4y}\)
\(\Leftrightarrow A=\left(x+\dfrac{1}{4x}\right)+\left(y+\dfrac{1}{4y}\right)+\left(\dfrac{3}{4x}+\dfrac{3}{4y}\right)\)
\(\Rightarrow A\ge2\sqrt{x.\dfrac{1}{4x}}+2\sqrt{y.\dfrac{1}{4y}}+\dfrac{3}{4}.\dfrac{4}{x+y}\)
\(\ge2.\sqrt{\dfrac{1}{4}}+2\sqrt{\dfrac{1}{4}}+\dfrac{3}{4}.\dfrac{4}{1}\)
\(=2.\dfrac{1}{2}+2.\dfrac{1}{2}+3=1+1+3=5\)
Vậy ta có đpcm. Dấu"=" xảy ra\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{4x}\\y=\dfrac{1}{4y}\\x=y\\x+y=1\end{matrix}\right.\) \(\Leftrightarrow x=y=\dfrac{1}{2}\left(tm\right)\)
CM
2 tháng 10 2017
Đáp án B.
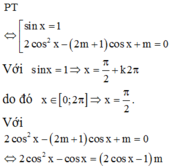
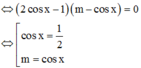
PT: cos x = 1 2 có 2 nghiệm thuộc trên đoạn 0 ; 2 π do đó để PT đã cho có 4 nghiệm thực thuộc đoạn 0 ; 2 π thì
TH1: m= cosx có 1 nghiệm thuộc đoạn 0 ; 2 π
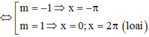
TH2: m= cosx có 2 nghiệm thuộc đoạn 0 ; 2 π trong đó có 1 nghiệm trùng
Vậy m= -1; m=0.
9 tháng 10 2021
Đặt \(A=x+y+z+\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\)
\(\Leftrightarrow A=x+y+z+\dfrac{9}{9x}+\dfrac{9}{9y}+\dfrac{9}{9z}\)
\(\Leftrightarrow A=x+y+z+\dfrac{1}{9x}+\dfrac{8}{9x}+\dfrac{1}{9y}+\dfrac{8}{9y}+\dfrac{1}{9z}+\dfrac{8}{9z}\)
\(\Leftrightarrow A=\left(x+\dfrac{1}{9x}\right)+\left(y+\dfrac{1}{9y}\right)+\left(z+\dfrac{1}{9z}\right)+\left(\dfrac{8}{9x}+\dfrac{8}{9y}+\dfrac{8}{9z}\right)\)
\(\Leftrightarrow A=\left(x+\dfrac{1}{9x}\right)+\left(y+\dfrac{1}{9y}\right)+\left(z+\dfrac{1}{9z}\right)+\dfrac{8}{9}.\left(\dfrac{1^2}{x}+\dfrac{1^2}{y}+\dfrac{1^2}{z}\right)\)
\(\Rightarrow A\ge2\sqrt{x.\dfrac{1}{9x}}+2\sqrt{y.\dfrac{1}{9y}}+2\sqrt{z.\dfrac{1}{9z}}+\dfrac{8}{9}.\dfrac{\left(1+1+1\right)^2}{x+y+z}\)
\(\Rightarrow A\ge2\sqrt{\dfrac{1}{9}}+2\sqrt{\dfrac{1}{9}}+2\sqrt{\dfrac{1}{9}}+\dfrac{8}{9}.\dfrac{3^2}{1}\)
\(\Rightarrow A\ge2.\dfrac{1}{3}.3+8=2+8=10\)
Vậy ta có BĐT cần chứng minh.
Dấu\("="\) xảy ra\(\Leftrightarrow x=y=z=\dfrac{1}{3}\)
