a. Lập pt của đtròn(C) tâm I(4;2) tiếp xúc với đg thẳng 3x+4y+5=0
b. Viết pt tiếp tuyến của đtròn(C) song song với trục Oy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CC
9 tháng 2 2020
(Chỉ mang t/c minh họa)
1/ Ta có I là trung điểm của AH (gt)
=> AI = AH = 1/2 AH (1)
BD _|_ AC tại D và H thuộc BC (gt)
=> △ABD vuông tại A
Xét △AHD vuông tại D có I là trung điểm của AH
=> DI = 1/2 AH (2)
Cmtt ta có : EI = 1/2 AH (3)
Từ (1)(2)(3) => AI = HI = DI = EI
=> 4 điểm A,D,H,E cùng thuộc 1 đtròn(I)
2/ Ta có : BD _|_ AC tại D (gt)
=> ^BDC = 90o
Cmtt ta có : ^BEC = 90o
=> ^BDC = ^BEC = 90o
=> 4 điểm B,E,D,C cùng thuộc 1 đtròn
12 tháng 2 2021
a) Xét tứ giác AOCM có
\(\widehat{MAO}\) và \(\widehat{MCO}\) là hai góc đối
\(\widehat{MAO}+\widehat{MCO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AOCM là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
nên A,O,C,M cùng nằm trên một đường tròn(đpcm)
Y
24 tháng 4 2023
\(PT\left(T\right)\) có dạng \(x^2+y^2-2ax-2by+c=0\)
\(\left\{{}\begin{matrix}A\left(-1;2\right)\in\left(T\right)\\B\left(1;2\right)\in\left(T\right)\\C\left(2;-3\right)\in\left(T\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(-1\right)^2+2^2+2a-4b+c=0\\1^2+2^2-2a-4b+c=0\\2^2+\left(-3\right)^2-4a+6b+c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2a-4b+c=-5\\-2a-4b+c=-5\\-4a+6b+c=-13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=0\\b=-\dfrac{4}{5}\\c=-\dfrac{41}{5}\end{matrix}\right.\)
\(\Rightarrow\)Tâm \(I\left(0;-\dfrac{4}{5}\right)\)
TM
23 tháng 5 2023
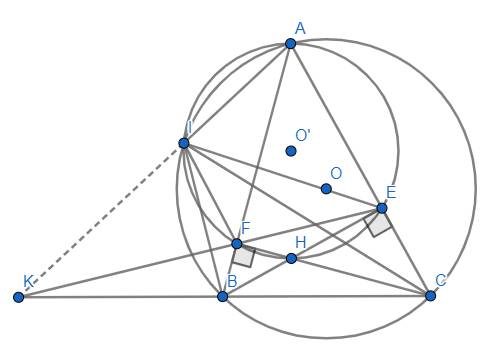
(a) Gọi \(O'\) là tâm đường tròn ngoại tiếp tứ giác \(AIFE.\)
Ta có : \(\hat{IEF}=\hat{IAF}\) (\(AIFE\) nội tiếp đường tròn \(\left(O'\right)\)) hay \(\hat{IEF}=\hat{IAB}.\)
Mà : \(\hat{IAB}=\hat{ICB}\) (hai góc nội tiếp đường tròn \(\left(O\right)\) cùng chắn cung \(IB\)).
Do đó, \(\hat{IEF}=\hat{ICB}.\)
Ta cũng có : \(\hat{FIE}=\hat{FAE}\) (\(AIFE\) nội tiếp đường tròn \(\left(O'\right)\)) hay \(\hat{FIE}=\hat{BAC}.\)
Mà : \(\hat{BAC}=\hat{BIC}\) (hai góc nội tiếp đường tròn \(\left(O\right)\) cùng chắn cung \(BC\)).
Do đó, \(\hat{FIE}=\hat{BIC}.\)
Xét \(\Delta IBC,\Delta IFE:\left\{{}\begin{matrix}\hat{ICB}=\hat{IEF}\left(cmt\right)\\\hat{BIC}=\hat{FIE}\left(cmt\right)\end{matrix}\right.\Rightarrow\Delta IBE\sim\Delta IFE\left(g.g\right)\) (đpcm).
(b) Mình tạm thời chưa nghĩ ra nhé:)
AT
1 tháng 6 2021
a) Vì AB là đường kính \(\Rightarrow\angle AEC=90\) mà \(\angle MOC=90\Rightarrow OMEC\) nội tiếp
b) Xét \(\Delta AMO\) và \(\Delta ACE:\) Ta có: \(\left\{{}\begin{matrix}\angle AOM=\angle AEC=90\\\angle CAEchung\end{matrix}\right.\)
\(\Rightarrow\Delta AMO\sim\Delta ACE\Rightarrow\dfrac{AM}{AO}=\dfrac{AC}{AE}\Rightarrow AM.AE=AO.AC=2R^2\)
Ta có: \(CD^2=CO^2+OD^2=2R^2\Rightarrow AM.AE+CD^2=4R^2\)
c) \(\Delta AMO\sim\Delta ACE\Rightarrow\dfrac{AC}{AE}=\dfrac{AM}{AO}=\dfrac{1}{2}=\dfrac{AD}{DN}\)
Xét \(\Delta ADN\) và \(\Delta AEC:\) Ta có: \(\left\{{}\begin{matrix}\angle ADN=\angle AEC=90\\\dfrac{AC}{AE}=\dfrac{AD}{DN}\end{matrix}\right.\)
\(\Rightarrow\Delta ADN\sim\Delta AEC\Rightarrow\angle AND=\angle ACE=\angle AMO\Rightarrow AMND\) nội tiếp
mà \(\angle ADN=90\Rightarrow\angle AMN=90\Rightarrow NM\bot AE\) mà \(CE\bot AE\)
\(\Rightarrow MN\parallel CE\)
d) Ta có: \(AM=\sqrt{AO^2+OM^2}=\dfrac{\sqrt{5}}{2}R\)
\(\Delta AMO\sim\Delta ACE\Rightarrow\dfrac{AE}{AC}=\dfrac{AO}{AM}=\dfrac{R}{\dfrac{\sqrt{5}}{2}R}=\dfrac{2}{\sqrt{5}}\)
\(\Rightarrow AE=\dfrac{4}{\sqrt{5}}R\)
AMND nt \(\Rightarrow\angle MAN=\angle MDN=\angle MDA=\angle MNA\Rightarrow\Delta MAN\) vuông cân tại M \(\Rightarrow MN=MA=\dfrac{\sqrt{5}}{2}R\)
Ta có: \(S_{ANE}=\dfrac{1}{2}NM.AE=\dfrac{1}{2}.\dfrac{\sqrt{5}}{2}R.\dfrac{4}{\sqrt{5}}R=R^2\)
về ý tưởng cơ bản là vậy,còn mình có tính toán gì sai thì bạn sửa nhé
