trong mặt phẳng oxy, biết d:3x+4y+4=0 cắt đường tròn C tại I(1;2) tại 2 điểm phân biệt A,B sao cho AB=8. tìm phương trình đường tròn C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


gọi H là trung điểm AB
=> \(IH=d_{\left(I,\Delta\right)}=\dfrac{\left|3\cdot2+4\cdot\left(-1\right)+3\right|}{\sqrt{3^2+4^2}}=1\)
\(S_{\Delta IAB}=2\cdot\left(\dfrac{1}{2}\cdot IH\cdot HA\right)=4\)
\(IH\cdot IA=4\Leftrightarrow1\cdot HA=4\Rightarrow HA=4\)
\(\Rightarrow R=IA=\sqrt{IH^2+HA^2}=\sqrt{1^2+4^2}=\sqrt{17}\)
\(\Rightarrow\) Phương trình đường tròn (x-2)2 +(y+1)2=17

(C) có tâm \(I\left(1;1\right)\) bán kính \(R=2\)
\(\Delta//d\Rightarrow\) phương trình \(\Delta\) có dạng: \(3x-4y+c=0\)
Áp dụng định lý Pitago: \(d\left(I;\Delta\right)=\sqrt{R^2-\left(\frac{AB}{2}\right)^2}=1\)
\(\Rightarrow\frac{\left|3.1-4.1+c\right|}{\sqrt{3^2+4^2}}=1\Leftrightarrow\left|c-1\right|=5\Rightarrow\left[{}\begin{matrix}c=6\\c=-4\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}3x-4y+6=0\\3x-4y-4=0\end{matrix}\right.\)
Do tính chất của đường tròn nên luôn có 2 đường thẳng đối xứng nhau qua tâm đường tròn thỏa mãn điều kiện bài toán, kiểu như trên hình, 2 dây cung cắt bởi 2 đường thẳng đối xứng qua tâm luôn dài bằng nhau
Chắc chắn cả 2 đáp án đều đúng, ko cái nào sai cả, nếu trong phương án chọn chỉ có 2 đáp án nằm riêng lẻ thì 1 là đáp án sai, 2 là bạn để ý kĩ lại dấu của 2 đáp án coi, có khi họ cho khác đi 1 chút xíu
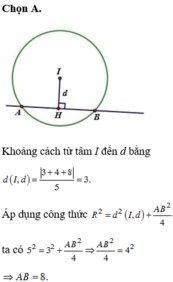

Gọi M là trung điểm AB
=> IM vuông góc AB
Ta có: AM = MB = AB : 2 = 4 cm
IM = d( I; d) = \(\frac{3.1+4.2+4}{\sqrt{3^2+4^2}}=3\) cm
Tam giác IMA vuông tại M
=> R = IA = \(\sqrt{3^2+4^2}=5\)
=> Phương trình đường tròn cần tìm: ( x - 1)^2 + ( y - 2)^2 = 25