Lập phương trình tổng quát của đường thẳng \(\Delta\) trong mỗi trường hợp sau :
a) \(\Delta\) đi qua điểm \(M\left(1;1\right)\) và có vectơ pháp tuyến \(\overrightarrow{n}=\left(3;-2\right)\)
b) \(\Delta\) đi qua điểm \(A\left(2;-1\right)\) và có hệ số góc \(k=-\dfrac{1}{2}\)
c) \(\Delta\) đi qua hai điểm \(A\left(2;0\right)\) và \(B\left(0;-3\right)\)


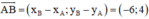
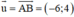 là một vtcp
là một vtcp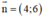 là một vtpt.
là một vtpt.
a,\(\Delta_a\) : 3 (x-1) - 2 (y-1) =3x-2y-1=0
b, \(\Delta_b\) : y=-\(\dfrac{1}{2}\)(x-2) =-\(\dfrac{1}{2}\)x =>\(\Delta_b\) : x+2y=0
c,\(\overrightarrow{AB}\)=(-2;-3) =>vtpt \(\overrightarrow{n}\)=(3;-2)
=>\(\Delta_c\): 3 (x-2) - 2(y-0) =0
=>\(\Delta_c\): 3x-2y-6=0
Lời giải
a) \(\Delta_a=3\left(x-1\right)-2\left(y-1\right)=3x-2y+5=0\)
b)\(\Delta_b:y=-\dfrac{1}{2}\left(x-2\right)-1=-\dfrac{1}{2}x\Rightarrow\Delta_b:x+2y=0\)
c) \(\Delta_c:\left(3+0\right)\left(x-2\right)+\left(0-2\right)\left(y-0\right)=3x-2y-6\)