Cho hàm số y = ( 2-m)x + 3
a) Vẽ đồ thị với m = 3.
b) Tìm m để hàm số đồng biến
c)Tìm m để đồ thị hàm số đi qua M(-1;1)
d)Tìm m để đường thẳng song song với y = -x +2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
26 tháng 12 2021
\(a,HS\text{Đ}B\Leftrightarrow a>0\\ \Leftrightarrow2m-4>0\\ \Leftrightarrow m>2\\ b,Thay:x_A=2;y_A=3.v\text{à}oHS:\\ y_A=\left(2m-4\right).x_A+m-1\\ \Leftrightarrow3=\left(2m-4\right).2+m-1\\ \Leftrightarrow5m=12\\ \Leftrightarrow m=\dfrac{12}{5}\\ c,m=3\Rightarrow y=\left(2.3-4\right)x+3-1=2x+2\)
Em tự vẽ đồ thi cho pt y=2x+2 nha!
23 tháng 11 2018
a) Hàm số đồng biến khi m - 2 > 0
<=> m > 2
Hàm số nghịch biến khi m - 2 < 0
<=> m < 2
23 tháng 11 2018
b) Vì A(1;-2) thuộc đồ thị
=> -2 = 1 ( m - 2 ) + 3
<=> -2 = m - 2 + 3
<=> m = 1
Vậy m = 1
16 tháng 4 2021
a) Để hàm số đạt giá trị nhỏ nhất bằng 0 khi x=0 thì 2m-1>0
\(\Leftrightarrow2m>1\)
hay \(m>\dfrac{1}{2}\)
16 tháng 4 2021
b) Để hàm số đồng biến khi x<0 và nghịch biến khi x>0 thì 2m-1<0
\(\Leftrightarrow2m< 1\)
hay \(m< \dfrac{1}{2}\)
30 tháng 1 2023
a: Để (1) đồng biến thì m-1>0
=>m>1
Để (1) nghịch biến thì m-1<0
=>m<1
b: Khi m=0 thì (1) sẽ là y=-x+2
c: y=(m-1)x+2-m
=mx-x+2-m
=m(x-1)-x+2
Điểm mà (1) luôn đi qua là:
x-1=0 và y=-x+2
=>x=1 và y=-1+2=1
11 tháng 10 2021
a: Để hàm số nghịch biến thì m-2<0
hay m<2
b: Thay x=3 và y=0 vào hàm số, ta được:
\(3m-6+m+3=0\)
hay \(m=\dfrac{3}{4}\)
3 tháng 2 2021
Để hàm số y=(m-5)x là hàm số bậc nhất thì \(m-5\ne0\)
hay \(m\ne5\)
1) Để hàm số y=(m-5)x đồng biến trên R thì m-5>0
hay m>5
Để hàm số y=(m-5)x nghịch biến trên R thì m-5<0
hay m<5
2) Để đồ thị hàm số y=(m-5)x đi qua A(1;2) thì
Thay x=1 và y=2 vào hàm số y=(m-5)x, ta được:
m-5=2
hay m=7(nhận)
Vậy: Để đồ thị hàm số y=(m-5)x đi qua A(1;2) thì m=7
Lời giải:
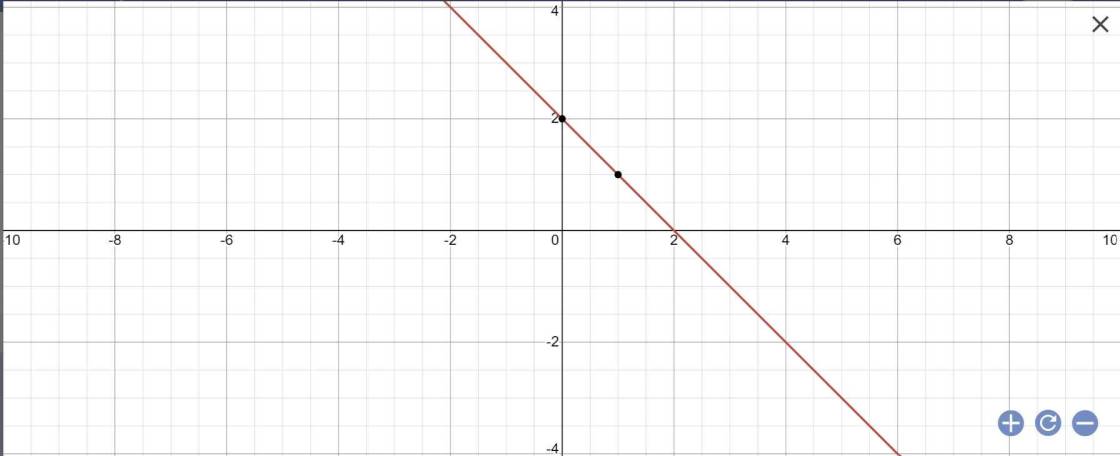
a. Với $m=3$ thì ptđt là $y=-x+3$. Đồ thị $y=-x+3$ như dưới đây:
b. Để hàm số đồng biến thì: $2-m>0$
$\Leftrightarrow m< 2$
c. Để đths đi qua $M(-1;1)$ thì $y_M=(2-m)x_M+3$
$\Leftrightarrow 1=(2-m)(-1)+3$
$\Leftrightarrow m=0$
d. Để đths đã cho với $y=-x+2$ song song với nhau thì:
$2-m=-1$
$\Leftrightarrow m=3$
giúp em với