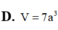cho hình vuông ABCD có A(1;1), điểm M thuộc cạnh CD sao cho DM=2CM. Biết phương trình cạnh BM: x+5y-18 =0. Tìm tọa độ các đỉnh của hình vuông biết C thuộc d: 2x-y+3=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 2 2019
a,Diện tích hình vuông ABCD là:
48 x 3 = 144 (cm2)
Ta có 12 x 12 = 144
Chu vi hình ABCD là
12 x 4 = 48 (cm)
b,Diện tích hình chữ nhật đó là
144 : 9 x 8 = 128(cm2)
Tổng của chiều dài và chiều rộng là
48 : 2 = 24 (cm)
Vậy hai số có tổng là 24 và tích là 128 là 16 và 8
Đáp số:a,48 cm
b,Chiều dài:16
Chiều rộng:8
10 tháng 5 2023
1: CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
=>(SCD) vuông góc (SAD)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 3 2023
Do ABCD là hình vuông \(\Rightarrow AB=d\left(A;BC\right)=\dfrac{\left|0-2.2-1\right|}{\sqrt{1^2+\left(-2\right)^2}}=\sqrt{5}\)
\(\Rightarrow AC=AB\sqrt{2}=\sqrt{10}\)
Do C thuộc BC \(\Rightarrow C\left(2c+1;c\right)\) \(\Rightarrow\overrightarrow{AC}=\left(2c+1;c-2\right)\)
\(\Rightarrow AC^2=\left(2c+1\right)^2+\left(c-2\right)^2=10\)
\(\Leftrightarrow5c^2-5=0\Rightarrow\left[{}\begin{matrix}c=1\\c=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}C\left(3;1\right)\\C\left(-1;-1\right)\end{matrix}\right.\)
Do C có hoành độ dương \(\Rightarrow C\left(3;1\right)\)
N là trung điểm AC \(\Rightarrow N\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)
12 tháng 8 2021
\(2,\)
Kẻ BH vuông góc với CD tại H
Xét hai tam giác BDH và BCH:
+) BH là cạnh chung
+) Góc BHD = góc BHC = 90 độ
+) DH = CH
=> Tam giác BDH = tam giác HCH (c.g.c)
=> BD = BC
Khác: DC = BC
=> BC = CD = DB => Tam giác BCD đều => Góc C = 60 độ
Mà: AB // CD => Góc B + góc C = 180 độ => Góc B = góc ABC = 180 độ - 60 độ = 120 độ
