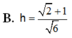
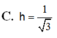
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
2: Ta có: \(\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}=\dfrac{a\left(a+b+c\right)}{b+c}+\dfrac{b\left(a+b+c\right)}{c+a}+\dfrac{c\left(a+b+c\right)}{a+b}-a-b-c=\left(a+b+c\right)\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)=a+b+c-a-b-c=0\)
1: Sửa đề: Cho \(x,y,z\ne0\) và \(\dfrac{1}{x}+\dfrac{2}{y}+\dfrac{1}{z}=\dfrac{2}{2x+y+2z}\).
CM:....
Đặt 2x = x', 2z = z'.
Ta có: \(\dfrac{2}{x'}+\dfrac{2}{y}+\dfrac{2}{z'}=\dfrac{2}{x'+y+z'}\)
\(\Leftrightarrow\dfrac{1}{x'}+\dfrac{1}{y}+\dfrac{1}{z'}=\dfrac{1}{x'+y+z'}\)
\(\Leftrightarrow\dfrac{1}{x'}-\dfrac{1}{x'+y+z'}+\dfrac{1}{y}+\dfrac{1}{z'}=0\)
\(\Leftrightarrow\dfrac{y+z'}{x'\left(x'+y+z'\right)}+\dfrac{y+z'}{yz'}=0\)
\(\Leftrightarrow\dfrac{\left(y+z'\right)\left(yz'+x'^2+x'y+x'z'\right)}{x'yz'\left(x'+y+z'\right)}=0\)
\(\Leftrightarrow\dfrac{\left(x'+y\right)\left(y+z'\right)\left(z'+x'\right)}{x'yz'\left(x'+y+z'\right)}=0\Leftrightarrow\left(2x+y\right)\left(y+2z\right)\left(2z+2x\right)=0\Leftrightarrow\left(2x+y\right)\left(y+2z\right)\left(z+x\right)=0\left(đpcm\right)\)
Đặt x/-4=k => x=-4k
y/-7=k => y=-7k
z/3=k => z=3k
=> A=8k+7k+15k / -8k+21k-18k
A=30k / -5k
=> A=-6
a) Hai mặt phẳng cắt nhau, vì 1: 2: (-1) ≠ 2: 3: (-7)
b) Hai mặt phẳng cắt nhau, vì: 1: (-2): 1 ≠ 2: (-1): 4
c) Hai mặt phẳng song song, vì: 1/2=1/2=1/2 ≠ -1/3
d) Hai mạt phẳng cắt nhau, vì: 3: (-2): 3 ≠ 9: (-6): (-9)
e) Hai mặt phẳng trung nhau, vì: 1/10=-1/(-10)=2/20=-4/(-40).
#rin
Cộng vế với vế ta được
x2 + 2y + 1 + y2 + 2x + 1 + z2 + 2x + 1 = 0
<=> (x2 + 2x + 1) + (y2 + 2y + 1) + (z2 + 2z + 1) = 0
<=> (x + 1)2 + (y + 1)2 + (z + 1)2 = 0
<=> \(\hept{\begin{cases}x+1=0\\y+1=0\\z+1=0\end{cases}}\Leftrightarrow x=y=z=-1\)
Khi đó A = x2000 + y2000 + z2000
= (-1)2000 + (-1)2000 + (-1)2000 = 1 + 1 + 1 = 3
Vậy A = 3
HD: Dễ thấy (P)//(Q). Gọi (R) là mặt phẳng song song và cách đều 2 mặt phằng (P) và (Q)
Chọn đáp án A