Trong không gian với hệ trục tọa độ Oxyz,qua 2 điểm M(1;-1;1) và N(0;-1;0) lập phương trình mặt phẳng \(\alpha\) cắt mặt cầu \(\left(S\right)\left(x+2\right)^2+\left(y+1\right)^2+\left(z-1\right)^2=5\) một thiết diện đường tròn mà diện tích hình tròn sinh bởi đường tròn có diện tích \(S=\pi\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án A
Hình chiếu của A x 0 ; y 0 ; z 0 lên các trục Ox, Oy, Oz lần lượt là các điểm A1 ( x 0 ;0;0), A2 (0; y 0 ;0), A3 (0;0; z 0 ).
Do đó hình chiếu của M (-2;-1;3) lên các trục Ox, Oy, Oz lần lượt là các điểm A (-2;0;0), B (0;-1;0), C (0;0;3).
Phương trình mặt phẳng theo đoạn chắn đi qua ba điểm A, B, C là: x - 2 + y - 1 + z 3 = 1

Đáp án C.
Gọi điểm H là hình chiếu của A 4 ; 1 ; − 2 trên mặt phẳng O x z , khi đó H 4 ; 0 ; − 2 .
Điểm A' đối xứng với A 4 ; 1 ; − 2 qua mặt phẳng O x z nên H 4 ; 0 ; − 2 là trung điểm AA' . Khi đó A ' 2 x H − x A ; 2 y H − y A ; 2 z H − z A → A ' 4 ; − 1 ; − 2

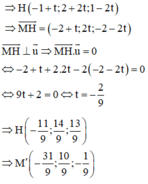
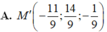
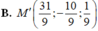
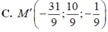
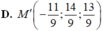
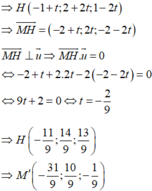



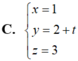
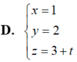

Mặt cầu (S) có tâm I(-2;-1;1) và bán kính \(R=\sqrt{5}\)
Gọi r là bán kinh đường tròn thiết diện, theo giả thiết ta có : \(S=\pi\Leftrightarrow r^2.\pi=\pi\Rightarrow r=1\)
Gọi d là khoảng cách từ I đến mặt phẳng \(\alpha\), ta có \(d^2=R^2-r^2=5-1\Rightarrow d=2\)
Mặt phẳng \(\alpha\), qua N (0;-1;0) có dạng \(Ax+B\left(y+1\right)+Cz=0\Leftrightarrow Ax+By+Cz+B=0\left(A^2+B^2+C^2\ne0\right)\)
Mặt khác, \(\alpha\) qua M(1;-1;1) nên thỏa mãn \(A+C=0\Rightarrow\text{ }\) \(\alpha:Ax+By-Az+B=0\)
Vì \(d=d\left(I,\alpha\right)=\frac{\left|-3A\right|}{\sqrt{2A^2+B^2}}=2\Leftrightarrow A^2=4B^2\Rightarrow\frac{A}{B}=\pm2\) vì \(A^2+B^2+C^2\ne0\)
Do đó có 2 mặt phẳng \(\alpha\), cần tìm là \(2x+y-2z+1=0\) và \(2x-y-2z-1=0\)