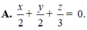
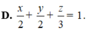
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Ta có n P → 1 ; 0 ; 0 ; n Q → 0 ; 1 ; − 1 suy ra n → = n P → ; n Q → = 0 ; 1 ; 1
Suy ra phương trình mặt phẳng cần tìm là: y + z − 5 = 0
Đáp án D
Ta có: A B → = ( - 3 ; - 2 ; 2 ) ; n ( P ) → = ( 1 ; - 3 ; 2 )
Khi đó: A B → ; n ( P ) → = 0 ; 8 ; 12 ⇒ n ( Q ) → = ( 0 ; 2 ; 3 )
Suy ra (Q): 2y + 3z – 11 = 0
Đáp án D
Ta có B A → = 3 ; 3 ; - 2 và (P) có véc tơ pháp tuyến n → = 1 ; - 3 ; 2 .
Gọi n ' → là véc tơ pháp tuyến của mặt phẳng (Q), để (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) thì: n → ⊥ n ' → ⊥ B A → ⇒ n ' = n → , B A → = 0 ; - 8 ; - 12 ⇒ Q : 0 x - 2 - 8 y - 4 - 12 z - 1 = 0 ⇔ 2 y + 3 z - 11 = 0
Đáp án A
Do (P) ⊥ AB nên mp(P) có một vectơ pháp tuyến là n P → = AB → = (-2; 1; 3). Mặt khác (P) đi qua điểm A nên phương trình của mặt phẳng (P) là:
-2(x - 1) + (y - 0) + 3(z + 2) = 0 ⇔ -2x + y + 3z + 8 = 0 ⇔ 2x - y - 3z - 8 = 0.
Vậy đáp án đúng là A.
Lưu ý. Khi ta viết phương trình mặt phẳng (P) bị nhầm ở cột z:
-2(x - 1) + (y - 0) + 3(z + 2) = 0 <> 2x - y - 3z - 4 = 0
thì ta được đáp án B.
Khi ta viết phương trình mặt phẳng bị nhầm giữa tọa độ của điểm A với tọa độ của vectơ pháp tuyến 1(x - (-2)) + 0(y - 1) -2(z - 3) = 0 <=> x - 2x + 8 = 0 thì ta được đáp án C.
Khi ta viết phương trình mặt phẳng đi qua B thì ta thu được đáp án D.
