Cho hình vuông ABCD có tâm I(4;-1) và pt 1 cạnh là 3x-y+5=0
a) Viết pt 2 đường chéo của hình vuông.
b) Viết tọa độ 4 đỉnh của hình vuông
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Trong mặt phẳng Oxy, cho hình vuông ABCD có đình M(-–-3;5), tâm I thuộc đường thẳng d : y =−x+5 và diện tích của hình vuông ABCD bằng 25 . Tim tọa độ các đỉnh của hình vuông ABCD, biết rằng tâm I có hoành độ dương
CM
27 tháng 6 2018
Đáp án D
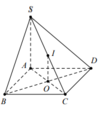
Vì O,I lần lượt là trung điểm của AC,SC. Suy ra OI//SA mà S A ⊥ A B C D ⇒ O I ⊥ A B C D .
S A ⊥ A B C D ⇒ S A ⊥ B D mà B D ⊥ A C ⇒ B D ⊥ S A C .
Ta có S A ⊥ C D A D ⊥ C D ⇒ C D ⊥ S A D ⇒ C D ⊥ S D ⇒ ∆ S C D vuông tại D.
Suy ra ID = IC tương tự ta được I B = I C ⇒ I A = I B = I C = I D .
BC không vuông góc với mặt phẳng (SCD) vì S C B ^ < 90 °
Vậy có hai khẳng định đúng là 1 và 3.
CM
28 tháng 10 2018
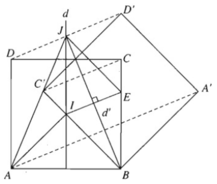
Gọi F là phép đối xứng qua đường trung trực d của cạnh AB, G là phép đối xứng qua đường trung trực d' của cạnh IE. Khi đó F biến AI thành BI, G biến BI thành BE. Từ đó suy ra phép dời hình có được bằng cách thực hiện liên tiếp hai phép biến hình F và G sẽ biến AI thành BE.
Hơn nữa gọi J là giao của d và d', thì dễ thấy JA = JB, JI = JE và 2(JI, JB) = (JI, JE) = 45 ο
(vì JE / /IB). Do đó theo kết quả của bài 1.21, phép dời hình nói trên chính là phép quay tâm J góc 45 ο
Lưu ý. Có thể tìm được nhiều phép dời hình biến AI thành BE.
b) F biến các điểm A, B, C, D thành B, A, D, C; G biến các điểm B, A, D, C thành B, A', D', C'. Do đó ảnh của hình vuông ABCD qua phép dời hình nói trên là hình vuông BA'D'C' đối xứng với hình vuông BADC qua d'
(AB) : 3x - y + 5 = 0
a) \(\left(BD\right):a_1x+b_1y+c=0\)
Vì góc tạo bởi ( AB ) và ( BD) là 45 độ nên
\(\cos\left(\left(AB\right),\left(BD\right)\right)=\frac{|3a_1-b_1|}{\sqrt{3^2+\left(-1\right)^2}\sqrt{a^2_1+b_1^2}}=\cos45^0=\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow\frac{|3a_1-b_1|}{\sqrt{10}.\sqrt{a_1^2+b_1^2}}=\frac{1}{\sqrt{2}}\)
\(\Leftrightarrow|3a_1-b_1|=\sqrt{5}.\sqrt{a_1^2+b_1^2}\)
\(\Leftrightarrow\left(3a_1-b_1\right)^2=5\left(a_1^2+b_1^2\right)\)
\(\Leftrightarrow9a^2-6a_1b_1+b_1^2=5a_1^2+5b_1^2\)
\(\Leftrightarrow4a^2-6a_1b_1-4b_1^2=0\)
\(\Leftrightarrow2a_1^2-3a_1b_1-2b_1^2=0\)
\(\Leftrightarrow2a_1^2-4a_1b_1+a_1b_1-2b_1^2=0\)
\(\Leftrightarrow\left(2a_1^2-4a_1b_1\right)+\left(a_1b_1-2b_1^2\right)=0\)
\(\Leftrightarrow2a_1\left(a_1-2b_1\right)+b_1\left(a_1-2b_1\right)=0\)
\(\Leftrightarrow\left(a_1-2b_1\right)\left(2a_1+b_1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}a_1-2b_1=0\\2a_1+b_1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}a_1=2b_1\\a_1=\frac{-b_1}{2}\end{cases}}}\)
Với a1 = 2b1 .... ( phần sau bn tự tính nha )
#phuongmato