Cho ba số x ; y ; z khác 0 thỏa mãn điều kiện \(\frac{y+z-x}{x}=\frac{z+x-y}{y}=\frac{x+y-z}{z}\)
Khi đó B = \(\left(1+\frac{x}{y}\right)\left(1+\frac{y}{z}\right)\left(1+\frac{z}{x}\right)\) có giá trị bằng .......
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Theo giả thiết ta có: x + 2 y = 10 2 x y = 16 ⇒ y = 8 x x + 16 x = 10 ⇒ 2 y = 16 x x 2 - 10 x + 16 = 0 ⇔ [ x = 8 x = 2 2 y = 16 x
⇒ [ x = 8 2 y = 2 x = 2 2 y = 8 ⇒ x - 2 y = 6 .

Chọn C.
Theo tính chất của cấp số cộng và cấp số nhân ta có
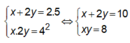
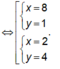
Vậy |x-2y| = 6


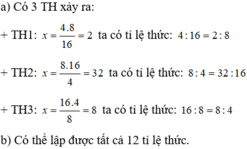
theo t/c dãy tỉ số=nhau:
\(\frac{y+z-x}{x}=\frac{z+x-y}{y}=\frac{x+y-z}{z}=\frac{y+z-x+z+x-y+x+y-z}{x+y+z}=\frac{x+y+z}{x+y+z}=1\)
=>x=y=z
\(1+\frac{x}{y}=\frac{x+y}{y}=\frac{y+y}{y}=\frac{2y}{y}=2\)
\(1+\frac{y}{z}=\frac{y+z}{z}=\frac{z+z}{z}=\frac{2z}{z}=2\)
\(1+\frac{z}{x}=\frac{z+x}{x}=\frac{x+x}{x}=\frac{2x}{x}=2\)
=>B=2.2.2=8
\(\frac{3x+3y+3z}{x+y+z}\)=\(\frac{1}{3}\)
\(\Leftrightarrow x=\frac{1}{2};y=\frac{1}{2};z=-\frac{1}{2}\)
\(\Leftrightarrow B=\left(1+\frac{\frac{1}{2}}{\frac{1}{2}}\right)\left(1+\frac{\frac{1}{2}}{\frac{-1}{2}}\right)\left(1+\frac{\frac{-1}{2}}{\frac{1}{2}}\right)\)=0