gọi x1; x2 là hai nghiệm của phương trình 5^(x-1)+5.0,2^(x-2)=26. Tính x1+x2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án B
P T ⇔ 2 2 x 2 − 5 2 x + 2 = 0 ⇔ 2 x = 2 2 x = 1 2 ⇔ x = 1 x = − 1 ⇒ x 1 = − 1 x 2 = 1 ⇒ x 2 − x 1 = 2.

Đáp án A
Phương pháp: Logarit hai vế, đưa về phương trình bậc hai một ẩn.
Cách giải:
![]()
![]()
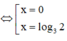
![]()

x1+x2=3; x1x2=-7
\(B=\left|x_1-x_2\right|=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\)
\(=\sqrt{3^2-4\cdot\left(-7\right)}=\sqrt{37}\)
\(F=\left(x_1^2+x_2^2\right)^2-2\left(x_1\cdot x_2\right)^2\)
\(=\left[3^2-2\cdot\left(-7\right)\right]^2-2\cdot\left(-7\right)^2\)
\(=23^2-2\cdot49=431\)

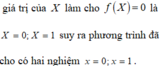


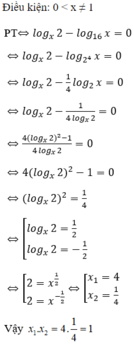
\(5^{x-1}+5.0,2^{x-2}=26\)
\(\Leftrightarrow5^{x-1}+\frac{5}{5^{x-2}}=26\)
\(\Leftrightarrow5^{x-1}+\frac{25}{5^{x-1}}=26\)
Đặt \(5^{x-1}=a\)
\(\Rightarrow a+\frac{25}{a}=26\)
\(\Leftrightarrow a^2-26a+25=0\)
\(\Leftrightarrow\orbr{\begin{cases}a=1\\a=25\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}5^{x-1}=1\\5^{x-1}=25\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\x-1=2\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\\x=3\end{cases}}\)