Cho parabol (P): y = x2 và đường thẳng (d): y = 2mx + 3. Gọi x1; x2 là hoành độ giao điểm của (d) và (P). Tìm m để |x1| + 3|x2| = 6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 3 2023
PTHĐGĐ là:
x^2+2mx+4m=0
Δ=(2m)^2-4*4m=4m^2-16m
Để (P) cắt (d)tại 2 điểm phân biệt thì 4m^2-16m>0
=>m>4 hoặc m<0
|x1|+|x2|=3
=>x1^2+x2^2+2|x1x2|=3
=>(x1+x2)^2-2x1x2+2|x1x2|=3
=>(-2m)^2-2*4m+2|4m|=3
=>4m^2-8m+8|m|=3
TH1: m>4
=>4m^2-8m+8m=3
=>4m^2=3
=>m^2=3/4
=>Loại
TH2: m<0
=>4m^2-8m-8m-3=0
=>4m^2-16m-3=0
=>\(m=\dfrac{4-\sqrt{19}}{2}\)
AT
10 tháng 6 2021
a) (d) đi qua \(A\left(1;5\right)\Rightarrow5=2m+2m-3\Rightarrow4m=8\Rightarrow m=2\)
\(\Rightarrow y=4x+1\)
b) pt hoành độ giao điểm \(x^2-2mx-2m+3=0\)
Để (d) tiếp xúc với (P) thì pt có nghiệm kép \(\Delta=0\)
\(\Delta=\left(2m\right)^2+8m-12=4m^2+8m-12\)
\(\Rightarrow4m^2+8m-12=0\Rightarrow m^2+2m-3=0\Rightarrow\left(m-1\right)\left(m+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-3\end{matrix}\right.\)
21 tháng 5 2021
a) Xét phương trình hoành độ giao điểm (d) và (P)
\(x^2 = 2(m+1)x - 4\)
\(<=> x^2 -2(m+1) + 4 = 0\) (1)
có \(\Delta' = [-(m+1)]^2 -4\)
\(\Delta' = (m+1)^2- 4\)
(d) và (P) cắt nhau tại hai điểm phân biệt
<=> Phương trình (1) có hai nghiệm phân biệt
<=> \(\Delta' \)> 0
<=> \((m + 1)^2 - 4 >0\)
<=> \((m+1)^2 >4\)
<=> \(\left[ \begin{array}{l}m+1 > 2\\m+1 <- 2\end{array} \right. \)
\(<=> \left[ \begin{array}{l}m > 1\\m < -3\end{array} \right. \)
b) Vì x1;x2 là hoành độ giao điểm của (d) và (P)
nên x1;x2 là hai nghiệm của phương trình (1)
Áp dụng hệ thức Viet có x1 + x2 = 2(m+1)
x1x2 = 4
Mà \(\sqrt{x_1} - \sqrt{x_2} = 2\)(x1;x2 \(\geq \) 0)
=> \((\sqrt{x_1} - \sqrt{x_2})^2 = 4\)
<=> x1 - 2x1x2 + x2 = 4
<=> (x1 + x2) - 2x1x2=4
<=> 2(m+1) - 2.4 = 4
<=> 2m + 2 - 8 = 4
<=> 2m = 10
<=> m = 5 (T/m)
AH
Akai Haruma
Giáo viên
21 tháng 5 2021
Đoạn \((\sqrt{x_1}-\sqrt{x_2})^2=4\)
\(\Rightarrow x_1-2\sqrt{x_1x_2}+x_2=4\) chứ bạn.
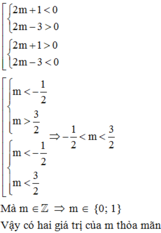
Phương trình hoành độ giao điểm của \(\left(d\right)\) và \(\left(P\right)\) là:
\(x^2=2mx+3\Leftrightarrow x^2-2mx-3=0\) (1)
Phương trình (1) có hệ số \(a.c=1.\left(-3\right)=-3< 0\) nên (1) luôn có hai nghiệm phân biệt \(x_1,x_2\).
Theo hệ thức Viete ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-3\end{matrix}\right.\)
Ta có: \(\left|x_1\right|+3\left|x_2\right|=6\)
Ta có hệ:
\(\left\{{}\begin{matrix}x_1x_2=-3\\\left|x_1\right|+3\left|x_2\right|=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{3}{x_2}\\\left|\dfrac{3}{x_2}\right|+3\left|x_2\right|=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{3}{x_2}\\x_2^2-2\left|x_2\right|+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x_2=-1,x_1=3\\x_2=1,x_1=-3\end{matrix}\right.\)
Với \(x_1=3,x_2=-1\Rightarrow x_1+x_2=2\Rightarrow m=1\).
Với \(x_1=-3,x_2=1\Rightarrow x_1+x_2=-2\Rightarrow m=-1\)
Phương trình hoành độ giao điểm của (d)(d) và (P)(P) là:
x2=2mx+3⇔x2−2mx−3=0x2=2mx+3⇔x2−2mx−3=0 (1)
Phương trình (1) có hệ số a.c=1.(−3)=−3<0a.c=1.(−3)=−3<0 nên (1) luôn có hai nghiệm phân biệt x1,x2x1,x2.
Theo hệ thức Viete ta có:
{x1+x2=2mx1x2=−3{x1+x2=2mx1x2=−3
Ta có: |x1|+3|x2|=6|x1|+3|x2|=6
Ta có hệ:
{x1x2=−3|x1|+3|x2|=6⇔⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩x1=−3x2∣∣∣3x2∣∣∣+3|x2|=6⇔⎧⎪⎨⎪⎩x1=−3x2x22−2|x2|+1=0{x1x2=−3|x1|+3|x2|=6⇔{x1=−3x2|3x2|+3|x2|=6⇔{x1=−3x2x22−2|x2|+1=0
⇔[x2=−1,x1=3x2=1,x1=−3⇔[x2=−1,x1=3x2=1,x1=−3
Với x1=3,x2=−1⇒x1+x2=2⇒m=1x1=3,x2=−1⇒x1+x2=2⇒m=1.
Với x1=−3,x2=1⇒x1+x2=−2⇒m=−1x1=−3,x2=1⇒x1+x2=−2⇒m=−1