Cho tam giác ABC cân tại A, Â = 800. Trên cạnh BC lấy điểm I sao cho góc BAI = 500; trên cạnh AC lấy điểm K sao cho góc ABK = 300. Hai đoạn thẳng AI và BK cắt nhau tại H. Chứng minh rằng D HIK cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 1 2016
kho.....................wa........................lanh.....................wa..................rich...................ung................ho..................minh...............cho.................do......................ret............to.............tich...............lai
2
28 tháng 10 2018
Mình vẽ hình hơi xấu bạn thông cảm nha0
Tam giác ABC cân tại A,góc A =80o => góc B= góc C=50o
Vẽ tam giác ABM ( M và C cùng nằm trên nửa nửa mat phẳng bờ AB)
Ta tính đc góc CBM=60o-50o=100
Xét tam giác AMI=tam giác BMI (c-c-c)
=> AMI=BMI=60o:2=30o
Trên tia BK lấy điểm N sao cho BN=MI
Tam giác BAN=tam giác MBI (c-g-c) => góc BAN=góc MBI=10o và AN=BI (1)
Tam giác IBA có 2 góc 50o nên cân tại I nên AI=BI (2)
Từ (1) và (2) => AN=AI (3)
Tam giác NAK có 2 góc 70o nên cân tại N => AN= NK (4)
Từ (3),(4) => AI=NK (5)
Tam giác HAN có 2 góc 40o nên cân tại H => HA=HN (6)
Từ (5),(6) => HI=HK => tam giác HIK cân (đpcm)
CH
Cô Hoàng Huyền
Admin
VIP
14 tháng 3 2018
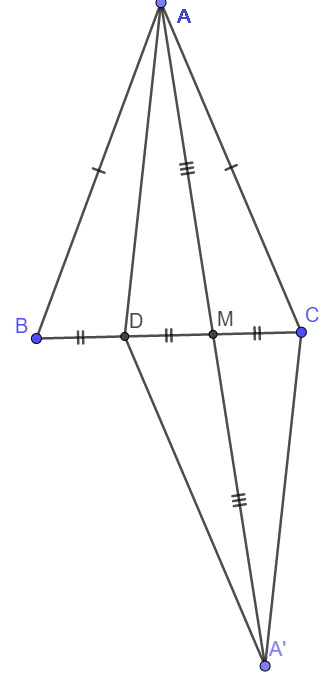
Gọi M là trung điểm DC và A' là điểm thuộc tia AM sao cho AM = MA'.
Khi đó ta thấy ngay \(\Delta AMC=\Delta A'MD\left(c-g-c\right)\)
\(\Rightarrow\widehat{MAC}=\widehat{MA'D}\) và AC = A'D.
Ta cũng có ngay \(\Delta ABD=\Delta ACM\left(c-g-c\right)\Rightarrow\widehat{BAD}=\widehat{CAM}\) và AB = AC
Kẻ AH vuông góc BC. Do tam giác ABC cân nên AH đồng thời là trung tuyến.
Vậy thì ta thấy ngay DH < BH nên theo quan hệ giữa đường xiên và hình chiếu ta có AD < AB
Suy ra AD < AC hay AD < DA'
Xét tam giác ADA' có AD < DA' nên theo quan hệ giữa cạnh và góc trong tam giác ta có :
\(\widehat{DAM}>\widehat{DA'M}\Rightarrow\widehat{DAM}>\widehat{MAC}\)
Lại có \(\widehat{DAM}+\widehat{MAC}=\widehat{CAD}\) nên \(\widehat{MAC}< \frac{1}{2}\widehat{CAD}\)
Vậy thì \(\widehat{BAD}< \frac{1}{2}\widehat{CAD}\left(đpcm\right)\)
