cho tam giác ABC có DT lad 18cm vuông; m,n lần lượt là trung điểm của BCvà AC.BN cắt AM tại G. chứng tỏ AGN=BGM.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 5 2023
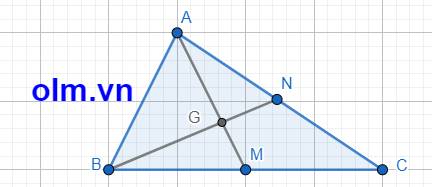
SABN = \(\dfrac{1}{2}\)SABC (Vì hai tam giác có chung đường cao hạ từ đỉnh B xuống đáyAC và AN = NC = \(\dfrac{1}{2}\)AC)
SABN = 18 : 2 = 9 (cm2)
Tương tự ta có: SABM = 9 (cm2)
⇒ SABN = SABM
SABN = SABG + SAGN
SABM = SABG + SBGM
⇒ SABG + SAGN = SABG + SBGM ⇒ SAGN = SBGM(đpcm)
NK
0
LK
1
14 tháng 11 2021
\(AC=\sin B\cdot BC=\dfrac{1}{2}\cdot18=9\left(cm\right)\)
2 tháng 5 2017
Chu vi tam giác ABC :
AHB + AHC = ABC
Thay số, ta được : 18+24 = 42 (cm)
S BGM=2/3*S BMN=2/3*1/2*S BNC=1/3*S BNC=1/6*S ABC
S AGN=2/3*S AMN=2/3*1/2*S AMC=1/3*S AMC=1/6*S ABC
=>S BGM=S AGN