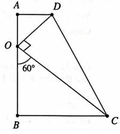
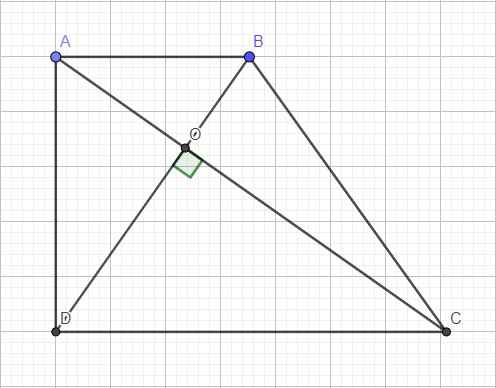
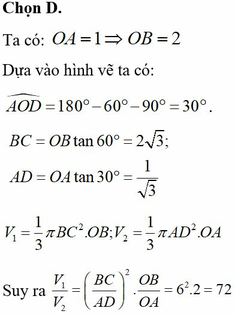Hình thang vuông ABCD vuông tại A, B; gọi O là điểm thuộc AB sao cho OB=2OA, OA=1, góc C O B ^ = 60 ∘ và tam giác COD vuông tại O. Kí hiệu V 1 , V 2 là thể tích các khối tròn xoay do tam giác OBC, OAD quay quanh đường thẳng AB. Tìm câu đúng?
A. V 2 = 72 V 1
B. V 2 = 36 V 1
C. V 1 = 36 V 2
D. V 1 = 72 V 2