cho hàm số y = f ( x ) = 4x2 - 7
a)tính f ( 1/2 ); f ( 3 ) ; f ( 0 ) ; f (-2 )
b) biết f ( x ) = 93 , tìm x
giúp mk nha mk tick cho
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) f(3) = 4.3^2 - 5 = 31
b) f(x) = -1
<=> 4x^2 - 5 = -1
<=> 4x^2 = 4
<=> x = 1 hoặc x = -1
c) f(x) = 4x^2 - 5 = 4(-x)^2 - 5 = f(-x)

Chọn C.
Ta có ![]()
![]()
![]()
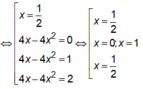
Do đó hàm số y = f ( 4 x - 4 x 2 ) có ba điểm cực trị là 0; 1 2 ;1

Ta có f x = 4 x 2 + 4 x + 3 2 x + 1 dx
= ∫ 2 x + 1 + 2 2 x + 1 d x = x 2 + x + ln x + 1 + C
Do f(0) = 1 nên c = 1. Suy ra f x = x 2 + x + ln 2 x + 1 + 1
Vậy a : b : c = 1 : 1 : 1
Đáp án B

Ta có ![]()
![]()
Đặt ![]() bất phương trình trở thành:
bất phương trình trở thành: ![]()
Kẻ đường thẳng y=5-2x qua các điểm (0;5), (1;3) nhận thấy t ∈ 0 ; 1 thì f '(t)<5-2t
Khi đó ![]()
Chọn đáp án B.

Cái này nhớ không nhầm là toán 7 :>
a) Gọi x1 và x2 là hai gtrị tương ứng của x
Giả sử x1<x2
Vì y=f(x) =-5x
\(\Rightarrow\)f(x1)=-5x1
\(\Rightarrow\)f(x2)=-5x2
mà x1<x2 \(\Rightarrow\)f(x1)>f(x2)
\(\Rightarrow\)Hs là hs nghịch biến
b) Vì y=f(x)=-5x
\(\Rightarrow\)f(x1)+4f(x2)
=-5x1+4(-5)x2
=-5(x1+4x2) (*)
\(\Rightarrow\)f(x1+4x2)=-5(x1+4x2) (**)
Từ (*), (**) \(\Rightarrow\)f(x1+4x2)=f(x1)+4f(x2)
c) Vì y=f(x)=-5x
\(\Rightarrow\)-f(x)=5x (*)
\(\Rightarrow\)f(-x)=-5(-x) =5x (**)
Từ (*) và (**) \(\Rightarrow\)-f(x) =f(-x)

Đặt t = f ( f ( x ) - 1 ) - 2 phương trình trở thành:
f ( t ) = 1 ⇔ t 4 - 4 t 2 + 1 = 1 ⇔ t = 0 ; t = ± 2
TH1: Nếu
t = 0 ⇔ f ( f ( x ) - 1 ) - 2 = 0 ⇔ f ( f ( x ) - 1 ) = 2
Đặt a=f(x)-1 phương trình trở thành:
f ( a ) = 2 ⇔ a 4 - 4 a 2 - 1 = 0 ⇔ a = ± 2 + 5
Nhận xét: Xét hàm số y = f ( x ) - 1 = x 4 - 4 x 2 có y c d = y ( 0 ) = 0 ; y c t = y ± 2 = - 4
Với a ∈ - 4 ; 0 phương trình y = a có bốn nghiệm thực phân biệt. Với a = 0 phương trình y = a có hai nghiệm thực phân biệt. Với a < -4 phương trình y = a vô nghiệm.
Áp dụng cho trường này có 2 + 4 = 6 nghiệm.
TH2: Nếu
t = - 2 ⇔ f ( f ( x ) - 1 ) - 2 = - 2 ⇔ f ( f ( x ) - 1 ) = 0
Đặt a=f(x)-1 phương trình trở thành:
f ( a ) = 0 ⇔ a 4 - 4 a 2 + 1 = 0 ⇔ a = ± 2 + 3
Trường hợp này có 2 + 2 + 4 + 4 = 12 nghiệm.
TH3: Nếu t = 2 ↔ f ( f ( x ) - 1 ) = 4 Đặt a=f(x)-1 phương trình trở thành:
f ( a ) = 4 ⇔ a 4 - a = ± 4 a 2 - 3 = 0 ⇔ a = ± 2 + 7
Trường hợp này có 2 + 4 = 6 nghiệm.
Vậy phương trình đã cho có tất cả 24 nghiệm thực phân biệt.
Chọn đáp án A.
cho hàm số y = f ( x ) = 4x2 - 7
a)tính f ( 1/2 ); f ( 3 ) ; f ( 0 ) ; f (-2 )
thay f(1/2);f(3);f(0);f(-2) vào hàm số f(x)=4x2-7
f(1/2)=4.(1/2)2-7=-6
f(3)=4.32-7=29
f(0)=4.02-7=-7
f(-2)=4.(-2)2-7=-24
cảm ơn ạ ^-^