Trong một mặt phẳng với hệ trục tọa độ oxy cho 2 đường thẳng d1: x+2y-5=0; d2 3x+my-1=0. Điều kiện của tham số m để góc tạo bởi hai đương thẳng bằng 45 độ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 5 2017
Chọn D.
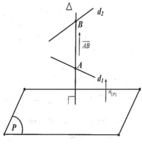
Vì d 1 không song song hoặc trùng với d 2 nên không tồn tại phép tịnh tiến nào biến d 1 thành d 2
15 tháng 3 2023
(d1): x+căn 3y=0
=>VTPT là \(\left(1;\sqrt{3}\right)\)
(d2): x+10=0
=>x+0y+10=0
=>VTPT là (1;0)
\(cos\left(d1;d2\right)=\left|\dfrac{1\cdot1+\sqrt{3}\cdot0}{\sqrt{1^2+3}\cdot\sqrt{1^2}}\right|=\left|\dfrac{1}{2}\right|=\dfrac{1}{2}\)
=>(d1;d2)=60 độ
17 tháng 2 2022
Tọa độ giao điểm của đường thẳng (d1) và (d2) là:
\(\left\{{}\begin{matrix}-2x+5y-8=0\\x+2y-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Để 3 đường thẳng trên đồng qua thì:
\(\left(m^2-1\right)x+3y-5-2m=0\\ \Leftrightarrow\left(m^2-1\right).1+3.2-5-2m=0\\ \Leftrightarrow m^2-1+6-5-2m=0\\ \Leftrightarrow m^2-2m=0\\ \Leftrightarrow m\left(m-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\)
17 tháng 2 2022
Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}-2x+5y-8=x+2y-5\\x+2y-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x+y=1\\x+2y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=1\end{matrix}\right.\)
Thay x=1 và y=2 vào (d3), ta được:
\(m^2-1+3\cdot2-5-2m=0\)
\(\Leftrightarrow m\left(m-2\right)=0\)
hay \(m\in\left\{0;2\right\}\)
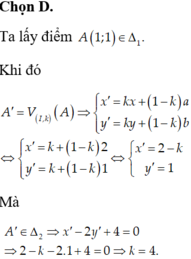
\(\overrightarrow{n_{d1}}=\left(1;2\right)\) ; \(\overrightarrow{n_{d2}}=\left(3;m\right)\)
Ta có: cos(d1;d2) = \(\left|cos(\overrightarrow{n_{d1};}\overrightarrow{n_{d2}})\right|\) = \(\frac{\sqrt{2}}{2}\)
=> \(\frac{3+2m}{\sqrt{\left(3+m^2\right)5}}\) = \(\frac{\sqrt{2}}{2}\) ⇔ 2(3 + 2m) = \(\sqrt{10\left(3+m^2\right)}\)
=> ĐK: 3 + 2m > 0 ⇔ m > \(\frac{-3}{2}\)