Bài 1 : Định m để hàm số
1. Y=2x^3-3(2m+1)x^2 + 6m(m+1) Đồng biến trên khoảng (2; dương vô cùng)
2. Y= x^3+ (m-1)x^2 -(2m^2 +3m+2)x Nghịch biến trên (2; dvc)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 6 2018
Chọn B
Phương pháp:
Tính y'.
Tìm m để 
Cách giải:
Ta có 
Xét phương trình y' = 0 
có 
Suy ra phương trình y' = 0 luôn có hai nghiệm 
Dễ thấy 
trong khoảng 
thì hàm số đồng biến.
Bài toán thỏa 
Do 
Vậy có 
giá trị của m thỏa mãn bài toán.
Chú ý:
Cách khác: Tìm m để 
Theo định lí Viet, ta có 
Hàm số đồng biến trên
(
2
;
+
∞
)
⇔
phương trình y' = 0 có hai nghiệm 
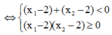
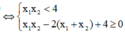
Vậy có 1001 số nguyên m thuộc khoảng (-10000;10000)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 6 2021
\(y=\dfrac{x^2-m^2+2m+1}{x-m}\) đúng không nhỉ?
\(y'=\dfrac{x^2-2mx+m^2-2m-1}{\left(x-m\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi và chỉ khi:
\(x^2-2mx+m^2-2m-1\ge0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=m^2-\left(m^2-2m-1\right)\le0\)
\(\Leftrightarrow m\le-\dfrac{1}{2}\)
AH
Akai Haruma
Giáo viên
26 tháng 8 2021
Bài 1:
a. $y=(m-2m+3m-2m+3)x-2=3x-2$
Vì $3\neq 0$ nên hàm này là hàm bậc nhất với mọi $m\in\mathbb{R}$
b. Vì $3>0$ nên hàm này là hàm đồng biến với mọi $m\in\mathbb{R}$
AH
Akai Haruma
Giáo viên
26 tháng 8 2021
Bài 2:
Đồ thị xanh lá cây: $y=-x+3$
Đồ thị xanh nước biển: $y=2x+1$
14 tháng 7 2021
Bài 1:
a) Để hàm số y=(k-2)x+k+3 là hàm số bậc nhất thì \(k\ne2\)
b) Để hàm số y=(k-2)x+k+3 đồng biến trên R thì k-2>0
hay k>2
Bài 2:
Thay \(x=-\dfrac{1}{2}\) và \(y=\dfrac{2}{3}\) vào (D), ta được:
\(\left(2m-3\right)\cdot\dfrac{-1}{2}-\dfrac{1}{2}=\dfrac{2}{3}\)
\(\Leftrightarrow\left(2m-3\right)\cdot\dfrac{-1}{2}=\dfrac{2}{3}+\dfrac{1}{2}=\dfrac{7}{6}\)
\(\Leftrightarrow2m-3=\dfrac{7}{6}:\dfrac{-1}{2}=\dfrac{-7}{6}\cdot\dfrac{2}{1}=-\dfrac{14}{6}=-\dfrac{7}{3}\)
\(\Leftrightarrow2m=\dfrac{-7}{3}+3=\dfrac{-7}{3}+\dfrac{9}{3}=\dfrac{2}{3}\)
hay \(m=\dfrac{1}{3}\)
N
1
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 8 2021
\(y'=3x^2-2\left(2m+1\right)x+m^2+2m=\left(x-m\right)\left(3x-m-2\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}x=m\\x=\dfrac{m+2}{3}\end{matrix}\right.\)
TH1: \(m=\dfrac{m+2}{3}\Rightarrow m=1\) hàm đồng biến trên R (thỏa mãn)
TH2: \(m< \dfrac{m+2}{3}\Rightarrow m< 1\) hàm đồng biến trên khoảng đã cho khi \(\dfrac{m+2}{3}\le0\Rightarrow m\le-2\)
TH3: \(m>\dfrac{m+2}{3}\Rightarrow m>1\) hàm đồng biến trên khoảng đã cho khi \(m\le0\) (ktm)
Vậy \(\left[{}\begin{matrix}m=1\\m\le-2\end{matrix}\right.\)
K
2 tháng 8 2020
Ta có \(y'=\frac{x^2-2mx+m^2}{\left(x-2m\right)^2},x\ne2m\)
Để y có hai khoảng đồng biến trên toàn miền xác định thì
\(y'\ge0,\forall x\ne2m\)
\(\Leftrightarrow x^2-4mx+m^2\ge0,\forall x\ne2m\)
\(\Leftrightarrow\Delta'\le0\Leftrightarrow4m^2-m^2\le0\)
\(\Leftrightarrow3m^2\le0\Leftrightarrow m=0\)
Câu tiếp theo:
y đồng biến trên\(\left(1,\infty\right)\Leftrightarrow y'\ge0,\forall x\in\left(1,+\infty\right)\)
\(\Leftrightarrow\hept{\begin{cases}f\left(x\right)=x^2-4mx+m^2\ge0,\forall x>1\\2m\notin\left(1,\infty\right)\end{cases}}\)
Để cj suy nghĩ mai lm tiếp=.=
K
2 tháng 8 2020
rõ ràng m=0 thì đk trên thõa mãn.
Với \(m=0:\Delta'=3m^2>0\) nên ta có:
\(f\left(x\right)\ge0,\forall x>1\Leftrightarrow x_1< x_2\le1\)
\(\Leftrightarrow\hept{\begin{cases}\Delta'>0\\f\left(1\right)\ge\\\frac{S}{2}-1< 0\end{cases}0}\)
\(f\left(1\right)\ge0\Leftrightarrow m^2-4m+1\ge0\Leftrightarrow m\le2-\sqrt{3}\)hay\(m\ge2+\sqrt{3}\)
\(\frac{S}{2}-1< 0\Leftrightarrow2m-1< 0\Leftrightarrow m< \frac{1}{2}\)
\(2m\notin\left(1,\infty\right)\Leftrightarrow2m\le1\Leftrightarrow m\le\frac{1}{2}\)
Vậy \(m\le2-\sqrt{3}\)là giá trị m cần tìm
