Cho hình chóp tứ giác đều S . ABCD có cạnh đáy AB = 10 cm ; cạnh bên SA = 12 cm .
Tính : a) Đường chéo AC .
b) Tính đường cao SO và thể tích hình chóp .
GIÚP ĐI MẤY BẠN MÌNH TICK CHO RỒI MÌNH KẾT BẠN NHA NHA NHA NHA :) ^_^ ........
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 5 2023
a: \(AC=\sqrt{10^2+10^2}=10\sqrt{2}\left(cm\right)\)
b: AO=5căn 2(cm)
=>\(SO=\sqrt{SA^2+AO^2}=\sqrt{194}\left(cm\right)\)
CM
15 tháng 12 2019
Chọn A
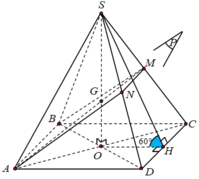
Gọi H là trung điểm cạnh CD và O là tâm hình vuông ABCD.
Ta có S. ABCD là hình chóp tứ giác đều nên các mặt bên hợp với đáy các góc bằng nhau
Giả sử S C D , A B C D ^ = S H O ^ = 60 o
Tam giác SHO vuông tại O có:
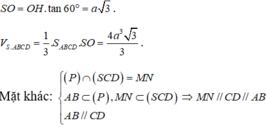
Mà G là trọng tâm tam giác SAC nên G cũng là trọng tâm tam giác SBD
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 6 2021
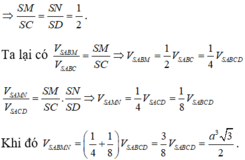
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\) \(\Rightarrow SO\perp BC\)
Gọi M là trung điểm BC \(\Rightarrow OM\perp BC\)
\(\Rightarrow BC\perp\left(SOM\right)\) \(\Rightarrow\left(SBC\right)\perp\left(SOM\right)\)
Trong tam giác vuông SOM, kẻ \(OH\perp SM\)
Do SM là giao tuyến (SOM) và (SBC) \(\Rightarrow OH\perp\left(SBC\right)\)
\(\Rightarrow CH\) là hình chiếu vuông góc của OC (hay AC) lên (SBC)
\(\Rightarrow\widehat{OCH}\) là góc giữa AC và (SBC)
\(\Rightarrow\widehat{OCH}=30^0\)
\(OC=\dfrac{1}{2}AC=a\sqrt{2}\) \(\Rightarrow OH=OC.sin30^0=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng:
\(\dfrac{1}{OH^2}=\dfrac{1}{SO^2}+\dfrac{1}{OM^2}=\dfrac{1}{SO^2}+\dfrac{4}{AB^2}\Rightarrow SO=a\)
\(V=\dfrac{1}{3}SO.AB^2=\dfrac{4a^3}{3}\)
