Câu 6. Cho biết ACB là góc nội tiếp chắn cung AB; BAx là góc tạo bởi một tia tiếp tuyến và một dây cung cùng chắn cung AB của đường tròn (O); biết ACB=80° thì BAx=
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 11 2017
(A) Sai. Góc nội tiếp là góc có đỉnh nằm trên đường tròn, hai cạnh chứa hai dây cung của đường tròn đó.
(B) Sai. Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung hoặc chắn hai cung bằng nhau.
(C) Sai. Trong một đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau.
(D) Sai. Trong một đường tròn, số đo của góc nội tiếp bằng một nửa số đo của góc ở tâm cùng chắn một cung.
(E) Đúng. Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
CM
11 tháng 1 2017
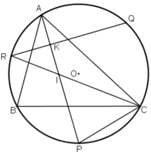
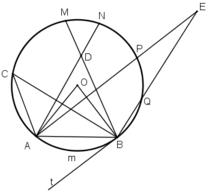
Gọi K là giao điểm của QR và AP.
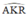là góc có đỉnh K nằm bên trong đường tròn
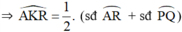
⇒ AP ⊥ QR.
HP
2
CM
3 tháng 6 2017
a) Đúng (theo hệ quả b).
b) Sai. Vì trong cùng một đường tròn, các góc nội tiếp cùng chắn 1 cung hoặc chắn các cung bằng nhau thì bằng nhau.
Trong một đường tròn, các góc nội tiếp bằng nhau chưa chắc cùng chắn một cung.
Kiến thức áp dụng
Định lý: Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
Hệ quả: Trong một đường tròn, các góc nội tiếp bằng nhau chắn các cung bằng nhau.
CM
21 tháng 3 2017
a) Đúng (theo hệ quả b).
b) Sai. Vì trong cùng một đường tròn, các góc nội tiếp cùng chắn 1 cung hoặc chắn các cung bằng nhau thì bằng nhau.
Trong một đường tròn, các góc nội tiếp bằng nhau chưa chắc cùng chắn một cung.
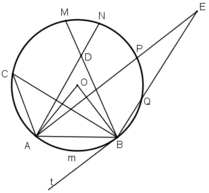
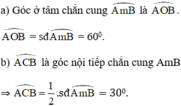
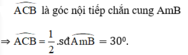
\(\widehat{BAx}=80^0\)