a)Cho biểu thức M = a + 2ab - b. Tính giá trị của M với |a|=1.5; b = 0.75
b) Xác định dấu của c bt rằng 2a^3bc trái dấu với -3a^5b^3c^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu a=-1,5; b=-0,75
Ta được: M=-1,5+2.(-1,5).(-0,75)-(-0,75)
=-1,5+2.1,125+0,75
=-1,5+2,25+0,75
=-1,5+3
=1,5
Nếu a=1,5; b=-0,75
Ta được: M=1,5+2.1,5.(-0,75)-(-0,75)
=1,5+3.(-0,75)+0,75
=1,5+(-2,25)+0,75
=-0,75+0,75
=0
Vậy.........
Hok tốt !!!

TH1: \(a< 0\Leftrightarrow a=-1,5\)
\(\Leftrightarrow M=-1,5+2.\left(-1,5\right)\left(-0,75\right)+0,75=1,5\)
TH2: \(a>0\Leftrightarrow a=1,5\)
\(\Leftrightarrow M=1,5+2.1,5.\left(-0,75\right)+0,75=0\)


Vì |a| = 1,5 nên a = 1,5 hoặc a = -1,5
Với a = 1,5; b = -0,75. Ta có:
M = 1,5 + 2.1,5( - 0,75) – (-0,75)
= 1,5 + ( -2,25) + 0,75
= (1,5 + 0,75) + (-2,25)
= 2,25 + (-2,25) = 0
N = 1,5 : 2 -2 : ( -0,75)
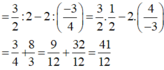
P = (-2) : (1,5)2 - (-0,75).(2/3)
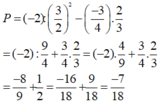
Với a = -1,5; b = -0,75 ta có:
M = - 1,5 + 2.(-1,5) ( - 0,75) – (-0,75)
= - 1,5 + ( 2,25) + 0,75
= (2,25+ 0,75) - 1,5
= 3 – 1,5 = 1,5
N = - 1,5 : 2 - 2 : ( -0,75)
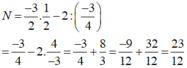
P = (-2) : (-1,5)2 — (-0,75).(2/3)
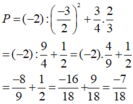

\(M=a^2+b^2+2a-2b-2ab+65\)
\(=\left(a^2-2ab+b^2\right)+2\left(a-b\right)+65\)
\(=\left(a-b\right)^2+2\left(a-b\right)+65\)
Ta có: \(a=5+b\Leftrightarrow a-b=5\)
\(\Rightarrow M=5^2+2.5+65=25+10+65=100\)
Vậy \(M=100.\)

l al = 1,5 => a = 1,5 hoặc a = -1,5
(+) a = 1,5
M = 1,5 + 2.1,5.-0,75 - - 0,75 = 1,5 + 3.-0,75 + 0,75 = 0
N , P tính tương tự
(+) a = -1,5 ; b = -0,75 thay vào ta có
M = ....
Tự làm tiếp nha

thay a=2.5 va b=-0.25 taco
M=a-2ab+b
=2.5-2*2.5*(-0.25)+(-0.25)
=2.5-5*(-0.25)+(-0.25)
=2.5-(-1.25)+(-0.25)
=3.75+(-0.25)=3.5
b)thay a=2.5 va b=-0.25 taco
N=a/5-5/b
=2.5/5-5/-0.25
=(2.5--0.25)/5
=2.75/5=0.55
a) Với b = 0.75, \(M=a+2a\times0.75-0.75=a+1.5a-0.75=2.5a-0.75.\)
Do \(|a|=1.5\)nên \(\orbr{\begin{cases}a=1.5\\a=-1.5\end{cases}}.\)
+) Nếu a = 1.5 thì \(M=2.5\times1.5-0.75=3.75-0.75=3.\)
+) Nếu a = -1.5 thì \(M=2.5\times\left(-1.5\right)-0.75=-3.75-0.75=-4.5.\)
b) Vì \(2a^3bc\)trái dấu với \(-3a^5b^3c^2\)nên ta có:
\(\left(2a^3bc\right)\times\left(-3a^5b^3c^2\right)\le0\)\(\Leftrightarrow-\frac{2}{3}a^8b^4c^3\le0\left(1\right).\)
Ta thấy rằng \(-\frac{2}{3}< 0\left(2\right).\)
Với mọi a, b là số thực, ta có: \(\hept{\begin{cases}a^8\ge0\\b^4\ge0\end{cases}\left(3\right)}\).
Từ (1),(2),(3) => \(c^3\ge0\Rightarrow c\ge0.\)
Vậy c là số không âm.