Có bao nhiêu cặp số (a ; b) thỏa mãn |a| + |b| = n với n \(\in\) N* ? Giải thích ?
Đáp số là có 4n số phải tìm chứ không phải không làm được. Yêu cầu trình bày cách giải
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
23 tháng 6 2016
a)Vì x,y ko âm =>x,y>0
=>ko tồn tại
b)Có vô số nghiệm x,y
Vd:1 và 0
-2 và 3
-3 và 4
.....
16 tháng 11 2016
Ta có từ số - 1357 tới 2016 có (2016 + 1357 + 1) = 3374 số
Cặp số 1 ta có 1 số
Cặp số 2 ta có 2 số
.....
Tổng các số trong tất cả các cặp là
\(1+2+3+...+n=\frac{n\left(n+1\right)}{2}\) (với n tự nhiên lớn hơn 0)
Ta nhận thấy rằng
\(\frac{n\left(n+1\right)}{2}\le3374\)
\(1\le n\le81\)
=> Có tất cả 81 cặp được chia
Từ đây ta thấy rằng có thể dùng \(\frac{81.82}{2}=3321\)để chia thành các cặp như trên
Số dư là \(3374-3321=53\)số
CM
12 tháng 7 2018
Đáp án cần chọn là: C
a 5 + 1 10 = − 1 b 2 a 10 + 1 10 = − 1 b 2 a + 1 10 = − 1 b 2 a + 1 . b = − 10
2a + 1 là số lẻ; 2a + 1 là ước của −10
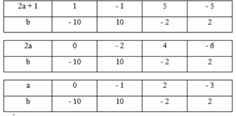
Vậy có 4 cặp số (a;b) thỏa mãn bài toán.
