BT1: Trên đường tròn (O; R) lấy A,B,C sao cho dây AC=R, dây BC= R √ 2, tia CO nằm giữa tia CA và CB. Tính sđ các GÓC: AOC, COB, AOB. Tính sđ cung BC
BT2: Cho tam giác ABC cân tại A, góc A nhọn. Đường tròn (O), đường kính BC cắt AB, AC tại D và E.
CM: BE = CD ⇒ góc BDE = góc DEC.
CM: cung CE = cung BD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 2 2022
Bài 1:
a: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó: BFEC là tứ giác nội tiếp
c: Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
Xét tứ giác BICD có
BI//CD(cùng vuông góc với AC)
CI//BD(cùng vuông góc với AB)
Do đó: BICD là hình bình hành
Bài 2:
a: Xét (O) có
MN=EF
OH là khoảng cách từ O đến dây MN
OK là khoảng cách từ O đến dây EF
Do đó: OH=OK
Xét ΔAHO vuông tại H và ΔAKO vuông tại K có
AO chung
OH=OK
Do đó: ΔAHO=ΔAKO
Suy ra: AH=AK
b: Xét ΔOHM vuông tại H và ΔOKE vuông tại K có
OM=OE
OH=OK
Do đó: ΔOHM=ΔOKE
Suy ra: HM=KE
Ta có: AM+MH=AH
AE+EK=AK
mà AH=AK
và HM=KE
nên AM=AE
16 tháng 5 2022
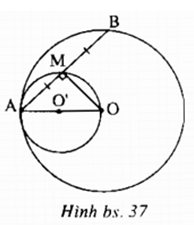
a: \(\widehat{AMO}=90^0\)
nên điểm M chuyển động trên đường tròn đường kính AO
b: Đường tròn (O') tiếp xúc trong với đường tròn (O)
