Cho hình thang ABCD, hai đáy AB, CD, AB<CD, kể doạn thẳng MN song song với hai đấy; M,N thuộc hai cạnh bên chia hình thang thành hai phần có diện tích bằng nhau. Chứng minh rằng: AB^2+CD^2=2MN^2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 9 2017
Theo tính chất của hình thang và cách đánh số đỉnh hình thang, hai đỉnh B, D nằm khác phía với đường thẳng AC, do đó A B → v à C D → ngược hướng.
AB < CD nên ABCD không là hình bình hành.
Đáp án C.
17 tháng 2 2017
1 đoạn thẳng sẽ nối với 9 đoạn thẳng còn lại để được hình thang
10 đoạn thẳng sẽ nối với : 10-1=9 đoạn thẳng
nhưng với cách nói trên thì số đoạn thẳng được tính hai lần
số hình thang có là 10x9:2= 45 hình
trừ đi hình thang ban đầu là hình ABCD ta được 44 hình thang được tạo thêm
15 tháng 1 2018
Đáy bé của hình thang là :
18 : 100 * 30 = 5,4 [ cm ]
Chiều cao của hình thang là :
[ 18 + 5,4 ] : 2 = 11,7 [ cm ]
Diện tích hình thang ABCD là :
[ 5,4 + 18 ] * 11,7 : 2 = 136,89 [ cm2 ]
Đáp số : 136,89 cm2
TT
0
CM
3 tháng 12 2017
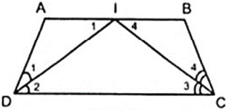
Áp dụng tính chất so le của AB//CD và giả thiết ta có:
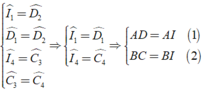
(vì trong một tam giác đối diện với hai góc bằng nhau là hai cạnh bằng nhau)
Cộng vế theo vế của ( 1 ) và ( 2 ) ta được: AD + BC = AB
Điều đó chứng tỏ tổng độ dài hai cạnh bên bằng độ dài của đáy AB của hình thang
