Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔABD vuông tại D vaf ΔACE vuông tại E có
AB=AC
góc BAD chung
=>ΔABD=ΔACE
=>AD=AE
b: Xét ΔABC có AD/AC=AE/AB
nên DE//BC
c: Xét ΔIBC có góc ICB=góc IBC
nên ΔIBC cân tại I
d: AB=AC
IB=IC
=>AI là trung trực của BC
=>AI vuông góc BC
a: Xét ΔBEC vuông tại E và ΔCDB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó: ΔBEC=ΔCDB
b: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
BD=CE
Do đó: ΔABD=ΔACE
Xét ΔBEK vuông tại E và ΔCDK vuông tại D có
EB=DC
\(\widehat{EBK}=\widehat{DCK}\)
Do đó: ΔBEK=ΔCDK
c: Xét ΔBAK và ΔCAK có
BA=CA
AK chung
BK=CK
Do đó: ΔBAK=ΔCAK
Suy ra: \(\widehat{BAK}=\widehat{CAK}\)
hay AK là tia phân giác của góc BAC
Xét tam giácBCE= tam giác CBD (cạnh huyền -mgóc nhọn)
góc ABC = góc ACB ( cân tại A)
BC chung
==> BD=CE
b) Tam giác BCE=tam giác CBD chứng minh ở câu a nên
góc BCE = góc DBC
--> IBC cân tại I
Sửa lại đề : A < 90*
a, Chứng minh
\(\Delta ABD=\Delta ACE\left(c.g.c\right)\)
\(\RightarrowĐPCM\)
b, CM được :
\(\widehat{ADE}\)\(=\)\(\widehat{ACB}\)\(=\)\(\frac{180'-\widehat{BAC}}{2}\)
\(\Rightarrow DE//BC\)
c, CM được : \(\widehat{IBC}=\widehat{ICB}\)
\(\RightarrowĐPCM\)
d, Gọi M là giao điểm của AI và BC ,
CM được AI là tia phân giác của góc \(\widehat{BAC}\), từ đó \(\widehat{AMB}\)\(=90'\)
\(\RightarrowĐPCM\)
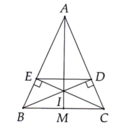
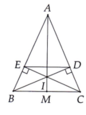
a ) Tam giác cân ABC có BD , CE là đường cao => BD , CE cũng là đường trung tuyến ứng với cạnh AC , AB
mà AB = AC => AE = AB = AD = AC
Xét \(\Delta ADB\)và \(\Delta AEC\)có :
AB = AC ( do tam giác ABC cân )
\(\widehat{ADB}=\widehat{AEC}\) \(\left(=90^o\right)\)( do \(BD\perp AC\), \(CE\perp AB\))
AD = AE ( cm trên )
nên \(\Delta ADB=\Delta AEC\)( c.g.c )
b ) Do \(\Delta ABC\) cân => \(\widehat{ABC}=\widehat{ACB}\)
\(\widehat{ABC}=\widehat{ABD}+\widehat{DBC}\)
\(\widehat{ACB}=\widehat{ACE}+\widehat{ECB}\)
Mà \(\widehat{ABD}=\widehat{ACE}\)( do \(\Delta ADB=\Delta AEC\)phần a ) => \(\widehat{DBC}=\widehat{ECB}\)
=> \(\Delta BOC\)cân
Mấy phần còn lại tự làm , hình dễ tự vẽ
A)Vì tam giác ABC cân tại A
=> ABC = ACB
=> AB = AC
Xét tam giác AEC (AEC = 90) và tam giác ADB(ADB=90) ta có :
AB = AC
Góc A chung
=> tam giác AEC = tam giác ADB ( ch-gn)
B) Tự xét tam giác ECB = tam giác DBC (cgv-gn)
=> EB = DC tương ứng
Xét tam giác EBO vuông tại E và tam giác DCO vuông tại D ta có :
EB = DC
EOB = DOC (đối đỉnh)
=> 2 tam giác trên bằng nhau
=> BO = OC tương ứng
=> tam giác BOC cân tại B