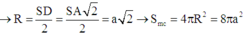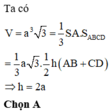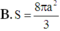Cho hình thang ABCD có 2 đáy là AB = 2a; CD = a. Hãy xác định vị trí điểm M trên đường thẳng CD sao cho Đường thẳng AM chia hình thang thành 2 phần có diện tích bằng nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2021
Khi quay quanh CD sẽ tạo ra hình khối gồm 2 khối:
- Khối trụ chiều cao \(AB=a\) bán kính đáy \(r=AD=a\Rightarrow V_1=\pi.AB^2.AD^2=\pi a^3\)
- Khối nón chiều cao \(CH=\dfrac{1}{2}CD=a\) bán kính đáy \(BH=AD=a\Rightarrow V_2=\dfrac{1}{3}\pi.a^2.a=\dfrac{\pi a^3}{3}\)
\(\Rightarrow V=V_1+V_2=\pi a^3+\dfrac{\pi a^3}{3}=\dfrac{4\pi a^3}{3}\)
CM
21 tháng 2 2019
Đáp án A
ABCD là hình thanh cân có AB = BC = CD = a; AD = 2a nên M là tâm của đáy ABCD.
SA = AD = 2a; SA ⊥ (ABCD) => tam giác SAD vuông cân tại A nên tâm mặt cầu ngoại tiếp hình chóp S.ABCD là trung điểm N của SD
