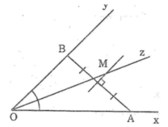
Cho Oz là phân giác góc xOy, các điểm A, B thuộc Ox; C, D thuộc Oy (theo thứ tự đó) sao cho AB = CD; M, N là trung điểm của AC, BD. Chứng minh MN // Oz
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 11 2017
Vì điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠(xOy).
Vì điểm M cách đều 2 điểm A và B nên M thuộc đường trung trực của AB.
Vậy M là giao điểm của đường trung trực của đoạn thẳng AB và tia phân giác Oz của ∠(xOy)
Do đó, có vô số điểm M thỏa mãn điều kiện trong câu a) khi OA = OB.
19 tháng 3 2021
+ Xét tam giác AHO ( góc A=90°) và tam giác BHO (góc B=90°) có: OH là cạnh chung
Góc BOH=AOH
=>TAM GIÁC AHO=BHO ( Cạnh huyền góc nhọn)
=>HA=HB
CC
11 tháng 1 2020
Xét \(\Delta OAB\)và \(\Delta OAC\)có :
\(\widehat{OBA}=\widehat{OCA\left(=90^o\right)}\)
OA là cạnh chung
\(\widehat{O_1}=\widehat{O_2}\left(gt\right)\)
\(\Rightarrow\Delta OAB=\Delta OAC\left(ch-gn\right)\)
