Cho tam giác ABC vuông tại A, biết AC=5; BC=10. Số đo góc ABC là:
A.300 B.750 C.450 D.600
(giải chi tiết)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 12 2017
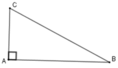
Áp dụng định lý Pytago cho tam giác vuông ABC ta có
BC2 = AC2 + AB2 => AB2 = 132 – 52
=> AB2 = 144 => AB = 12 cm
Suy ra SABC= A C . A B 2 = 5.12 2 = 30 cm2.
Đáp án cần chọn là: A
CM
7 tháng 4 2018
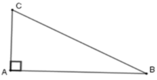
Áp dụng định lý Pytago cho tam giác vuông ABC ta có:
BC2 = AC2 + AB2 => AB2 = 52 – 32
=> AB2 = 16 => AB = 4 cm
Suy ra SABC= A C . A B 2 = 3.4 2 = 6 cm2.
Đáp án cần chọn là: C
NL
0
NL
0
NL
0
2 tháng 12 2021
\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)
CM
11 tháng 7 2017
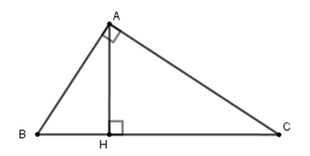
Theo giả thiết AB : AC = 5 : 12
Suy ra A B 5 = A C 12 = A B + A C 5 + 12 = 34 17 = 2 . Do đó AB = 5.2 = 10 (cm);
AC = 2.12 = 24 (cm)
Tam giác ABC vuông tại A, theo định lý Pytago ta có:
B C 2 = A B 2 + A C 2 = 10 2 + 24 2 = 676 , suy ra BC = 26cm
Đáp án cần chọn là: C
Chọn A