Cho hình chữ nhật ABCD . Trên CB và AD lấy điểm M và N sao cho AM = CN . Trên AB lấy K tùy ý ( khác A ; B ) MN cắt KD và KC lần lượt tại E và F . So sánh diện tích KEF và diện tích DME = diện tích CNF
Ai làm đúng mình cho 5 like ! ( nói thật )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 9 2019
S(KCD) = CD x BC X 1/2 = 1/2 S(ABCD)
-S(ABNM) = S(CDMN) = 1/2 s(ABCD) ( Vì AM = NC, DM = BN, AB = CD)
=> S(ABNM) = S(KCD)
=> S(CDEF) = S(AKEM) + S(BKFN) ( cùng chung S(KEF)
- Mà S(ABNM) = S(CDMN) => S(KEF) = S(DME) + S(CNF) ( cùng bớt S(CDEF) = S(AKEM) + S(BKFN))
CM
9 tháng 8 2018
-S(KCD) = CD x BC X 1/2 = 1/2 S(ABCD) -S(ABNM) = S(CDMN) = 1/2 s(ABCD) ( Vì AM = NC, DM = BN, AB = CD) => S(ABNM) = S(KCD) => S(CDEF) = S(AKEM) + S(BKFN) ( cùng chung S(KEF) - Mà S(ABNM) = S(CDMN) => S(KEF) = S(DME) + S(CNF) ( cùng bớt S(CDEF) = S(AKEM) + S(BKFN))
13 tháng 10 2016
Sơ đồ minh họa:
Phân tích: Ta thấy tam giác \(KDC\) và tứ giác \(MNCD\) có phần chung là tứ giác \(EFCD\).
Vậy để chứng tỏ: \(S_{KEF}=S_{MED}+S_{FNC}\) ta cần chứng tỏ \(S_{KDC}=S_{MNCD}\)
Giải tóm tắt:
\(S_{KDC}=DC\times BC\div2=\frac{1}{2}\times S_{ABCD}\) (1)
Vì \(ABCD\) là hình chữ nhật nên tứ giác \(MNCD\) là hình thang và có diện tích là:
\(S_{MNCD}=\left(MD+NC\right)\times DC\div2=\)
\(=AD\times DC\div2=\frac{1}{2}\times S_{ABCD}\) (2)
Từ (1) và (2) ta có: \(S_{KDC}=S_{MNCD}\)
Tam giác \(KDC\) và hình thang \(MNCD\) có phần chung là tứ giác \(EFCD\), suy ra:
\(S_{KEF}=S_{MED}+S_{FNC}\)
CM
23 tháng 8 2019
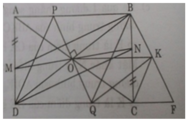
a) Ta có AD = BC; AD // BC (gt), AM = CN (gt)
⇒ AD – AM = BC – CN
Hay DM = BN
Lại có DM // BN
Do đó MNDN là hình bình hành ⇒ BM // DN
CM
12 tháng 10 2019
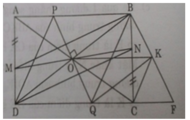
d) Gọi F là giao điểm của BK và QC. Ta có O là trung điểm của BD và OQ // BK (gt) nên Q là trung điểm của DF.
Lại có QK // BD (gt); Q là trung điểm của DF ⇒ K là trung điểm của BF.
CK là trung tuyến của tam giác vuông BCF ⇒ CK = BK = BC/2.
Ta có QK là đường trung bình của tam giác
⇒ QK = BO = BD/2; QK // BO
⇒ Tứ giác OBKQ là hình bình hành
Mặt khác ∠(OBQ) = 90o ⇒ OBKQ là hình chữ nhật
⇒ ∠(OBK) = 90o
Xét ΔOCK và ΔOBK có
CK chung
OC = OB (tính chất đường chéo hình chéo hình chữ nhật)
CK = BK (cmt)
Vậy ΔOCK = ΔOBK (c.c.c) ⇒ ∠OCK = ∠OBK = 90o hay AC ⊥ CK.
