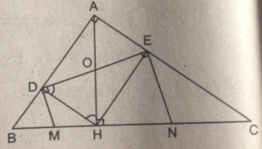
Cho tam giác ABC vuông tại A. Kẻ đường cao AH. Gọi D, E là các hình chiếu của H trên AB, AC và M, N theo thứ tự là các trung điểm của các đoạn thẳng BH, CH.
a) Chứng minh AH = DE; AH.BC = AB.AC
b) Chứng minh tứ giác MDEN là hình thang vuông.
c) Gọi P là giao điểm của đường thẳng DE với đường cao AH và Q là trung điểm của đoạn thẳng MN. Chứng minh PQ⊥DE .
d) Chứng minh P là trực tâm ∆ABM.
e) Cho K là điểm nằm giữa BC. Tìm vị trí của K để AK có độ dài ngắn nhất
f) Chứng minh SABC = 2.SMDEN .

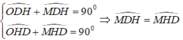


a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)