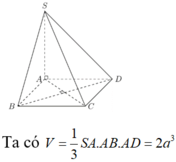
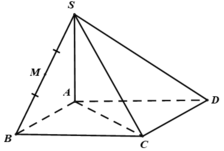
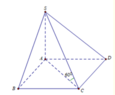
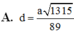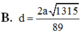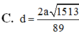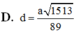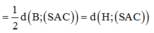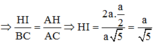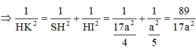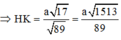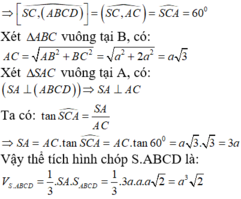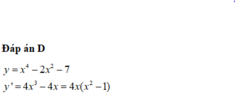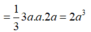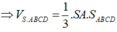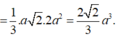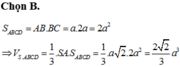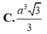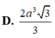Cho hình chóp S.ABCD có đáy hình chữ nhật, AB=a; AD=2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45 0 . Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC)